题目内容
13.已知等差数列{an}的公差d≠0,且a3,a5,a15成等比数列,若a1=3,Sn为数列an的前n项和,则an•Sn的最小值为( )| A. | 0 | B. | -3 | C. | -20 | D. | 9 |
分析 由等差数列{an}的通项公式及等比数列性质列出方程,求出d=-2或d=0,由此能求出an•Sn的最小值.
解答 解:∵等差数列{an}的公差d≠0,且a3,a5,a15成等比数列,a1=3,
∴(3+4d)2=(3+2d)(3+14d),
解得d=-2或d=0,
当d=0时,an=3,Sn=3n,anSn=9n,
当n=1时,an•Sn取最小值9;
当d=-2时,an=3+(n-1)(-2)=5-2n,
Sn=3n+$\frac{n(n-1)}{2}×(-2)$=4n-n2,
an•Sn=(5-2n)(4n-n2)=2n3-13n2+20n,
设f(n)=2n3-13n2+20n,则f′(n)=6n2-26n+20=6(n-$\frac{13}{6}$)2-$\frac{49}{6}$,
∴当n=3时,an•Sn取最小值:2×27-13×9+20×3=-3.
综上,an•Sn取最小值为-3.
故选:B.
点评 本题考查等差数列的第n项与前n项和的积的最小值的求法,是中档题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
1.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤2\\ ax-y-2a≤0\end{array}\right.$,z=x+2y的最小值为-2,则a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
8.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}x,x>0}\\{{3}^{x},x≤0}\end{array}\right.$,则f(f(9))的值为( )
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
4.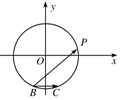 已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
 已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}+1$ |
2.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 6 | B. | 9 | C. | 12 | D. | 18 |