题目内容
10.已知α为第二象限角,sin(π+α)=-$\frac{1}{3}$,则tanα=( )| A. | -$\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由已知利用诱导公式求得sinα,再由同角三角函数的基本关系式得答案.
解答 解:∵sin(π+α)=-$\frac{1}{3}$,且α为第二象限角,
∴sinα=$\frac{1}{3}$,cosα=-$\sqrt{1-si{n}^{2}α}=-\frac{2\sqrt{2}}{3}$,
∴tanα=$-\frac{\sqrt{2}}{4}$.
故选:A.
点评 本题考查三角函数的化简求值,考查同角三角函数基本关系式及诱导公式的应用,是基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤2\\ ax-y-2a≤0\end{array}\right.$,z=x+2y的最小值为-2,则a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
5.设复数$z=\frac{{2{i^3}}}{i-1}$(i为虚数单位),z则的虚部为( )
| A. | i | B. | -i | C. | -1 | D. | 1 |
15.下列函数中,最小正周期为π且在(0,$\frac{π}{2}$)是减函数的是( )
| A. | y=cos(2x+$\frac{π}{2}$) | B. | y=|sin(x+$\frac{π}{3}$)| | C. | y=2cos2x-3 | D. | y=-tan2x |
2.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
19.袋中有大小,形状相同的红球,黑球各一个,现有放回地随机摸取3次,每次摸出一个球.若摸到红球得2分,摸到黑球得1分,则3次摸球所得总分为5分的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
20.已知直线l1:ax+2y-1=0,直线l2:8x+ay+2-a=0,若l1∥l2,则实数a的值为( )
| A. | ±4 | B. | -4 | C. | 4 | D. | ±2 |
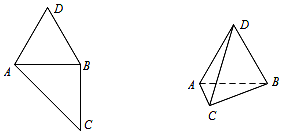 如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.
如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.