题目内容
9.函数$f(x)=Asin(ωx+\frac{π}{4})(ω>0)$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{3π}{4}$个单位 |
分析 函数$f(x)=Asin(ωx+\frac{π}{4})(ω>0)$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列,可知周期T=$\frac{2π}{3}$,可得ω的值,根据三角函数的平移变换规律可得结论.
解答 解:由题意,函数$f(x)=Asin(ωx+\frac{π}{4})(ω>0)$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列,可知周期T=$\frac{2π}{3}$,
那么:ω=$\frac{2π}{T}=2π×\frac{3}{2π}=3$.
则f(x)=Asin(3x+$\frac{π}{4}$)=Asin3(x+$\frac{π}{12}$)
要得到g(x)=Acos3x,
即Acos3x=Asin(3x+$\frac{π}{2}$)=Asin3(x+$\frac{π}{6}$)
由题意:可得:f(x)向左平移$\frac{π}{12}$可得g(x)
故选A
点评 本题主要考查函数y=Asin(ωx+∅)的图象变换规律,比较基础.

练习册系列答案
相关题目
19.一个几何体的三视图如图所示,则其体积为( )


| A. | π+2 | B. | 2π+4 | C. | π+4 | D. | 2π+2 |
17.($\sqrt{x}$-2x)5的展开式中,含x3项的系数是( )
| A. | -10 | B. | -5 | C. | 5 | D. | 10 |
1.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤2\\ ax-y-2a≤0\end{array}\right.$,z=x+2y的最小值为-2,则a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
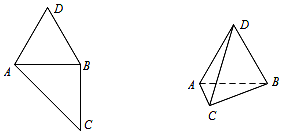 如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.
如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.