题目内容
已知x,y满足不等式
,那么z=2x+y的最大值是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,代入最优解的坐标得答案.
解答:
解:由约束条件
作出可行域如图,

由z=2x+y,得y=-2x+z,由图可知,当直线y=-2x+z过A(2,0)时,直线在y轴上的截距最大,z最大等于2×2+0=4.
故答案为:4.
|

由z=2x+y,得y=-2x+z,由图可知,当直线y=-2x+z过A(2,0)时,直线在y轴上的截距最大,z最大等于2×2+0=4.
故答案为:4.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
班级需要在甲、乙、丙三位同学中随机的抽取两位参加一项活动,则正好抽到的是甲乙的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
三个数70.3,0.37,ln0.3从大到小的顺序是( )
| A、70.3,ln0.3,0.37 |
| B、70.3,0.37,ln0.3 |
| C、ln0.3,70.3,0.37 |
| D、0.37,70.3,ln0.3 |
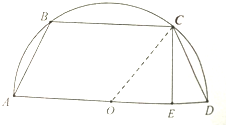 在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.
在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.