题目内容
16．下列函数中，以π为周期且在区间（0，$\frac{π}{2}$）上为增函数的是（ ）| A． | y=sin$\frac{x}{2}$ | B． | y=sin x | C． | y=-tan x | D． | y=-cos 2x |
分析 根据三角函数的图象及性质，依次判断各选项即可．
解答 解：对于A：y=sin$\frac{x}{2}$，其周期T=$\frac{2π}{\frac{1}{2}}=4π$，∴A不对．
对于B：y=sin x，其周期T=$\frac{2π}{1}=2π$，∴B不对．
对于C：y=-tan x，其周期T=$\frac{π}{1}=π$，在区间（0，$\frac{π}{2}$）上为减函数，∴C不对．
对于D：y=-cos 2x，其周期T=$\frac{2π}{2}=π$，cos 2x在区间（0，$\frac{π}{2}$）上为减函数，则y=y=-cos 2x，在区间（0，$\frac{π}{2}$）上为增函数，故选D．
点评 本题主要考查三角函数的图象和性质，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
6．已知函数$f（x）=\left\{\begin{array}{l}（{a-1}）x+4-2a，x＜1\\ 1+{log_2}x，x≥1\end{array}\right.$，若f（x）的值域为R，则实数a的取值范围是（ ）
| A． | （1，2] | B． | （-∞，2] | C． | （0，2] | D． | [2，+∞） |
4．2016年美国总统大选过后，有媒体从某公司的全体员工中随机抽取了200人，对他们的投票结果进行了统计（不考虑弃权等其他情况），发现支持希拉里的一共有95人，其中女员工55人，支持特朗普的男员工有60人．
（Ⅰ）根据已知条件完成下面的2×2列联表：据此材料，是否有95%的把握认为投票结果与性别有关？
（Ⅱ）若从该公司的所有男员工中随机抽取3人，记其中支持特朗普的人数为X，求随机变量X的分布列和数学期望．（用相应的频率估计概率）
附：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
（Ⅰ）根据已知条件完成下面的2×2列联表：据此材料，是否有95%的把握认为投票结果与性别有关？
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
附：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11．已知函数f（x）=2sin（2x-$\frac{π}{6}$）+a，a为常数
（1）求函数f（x）的最小正周期；
（2）若x∈[0，$\frac{π}{2}$]时，f（x）的最小值为-2，求a的值．
（1）求函数f（x）的最小正周期；
（2）若x∈[0，$\frac{π}{2}$]时，f（x）的最小值为-2，求a的值．
1．已知函数f（x）=cos（2x+φ），且${∫}_{0}^{\frac{2}{3}π}$f（x）dx=0，则下列说法正确的是（ ）
| A． | f（x）的一条对称轴为x=$\frac{5π}{12}$ | |
| B． | 存在φ使得f（x）在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上单调递减 | |
| C． | f（x）的一个对称中心为（$\frac{5π}{12}$，0） | |
| D． | 存在φ使得f（x）在区间[$\frac{π}{12}$，$\frac{7π}{12}$]上单调递增 |
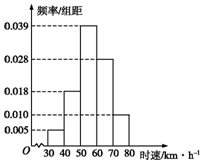某时段内共有100辆汽车经过某一雷达地区，汽车时速的频率分布直方图如图所示，则时速不低于60km/h的汽车数量为（ ）
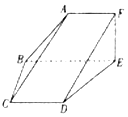如图，平面ABEF⊥平面CBED，四边形ABEF为直角梯形，∠AFE=∠FEB=90°，四边形CBED为等腰梯形，CD∥BE，且BE=2AF=2CD=2BC=2EF=4．