题目内容
6.已知函数$f(x)=\left\{\begin{array}{l}({a-1})x+4-2a,x<1\\ 1+{log_2}x,x≥1\end{array}\right.$,若f(x)的值域为R,则实数a的取值范围是( )| A. | (1,2] | B. | (-∞,2] | C. | (0,2] | D. | [2,+∞) |
分析 利用函数的值域范围,结合分段函数求解最值,推出结果即可.
解答 解:函数$f(x)=\left\{\begin{array}{l}({a-1})x+4-2a,x<1\\ 1+{log_2}x,x≥1\end{array}\right.$,当x≥1时,f(x)=1+log2x≥1,
x<1时,f(x)=(a-1)x+4-2a必须是增函数,最大值≥1,才能满足f(x)的值域为R,
可得$\left\{\begin{array}{l}{a-1>0}\\{a-1+4-2a≥1}\end{array}\right.$,解得a∈(1,2].
故选:A.
点评 本题考查分段函数的应用,函数的最值的求法以及函数的单调性的应用,考查计算能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
1.已知实数x,y满足不等式组$\left\{\begin{array}{l}x-3y+5≥0\\ 2x+y-4≤0\\ y+2≥0\end{array}\right.$则z=x+y的最小值为-13.
16.下列函数中,以π为周期且在区间(0,$\frac{π}{2}$)上为增函数的是( )
| A. | y=sin$\frac{x}{2}$ | B. | y=sin x | C. | y=-tan x | D. | y=-cos 2x |
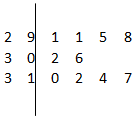 如图是根据我省的统计年鉴中的资料做成的2007年至2016年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到2007年至2016年我省城镇居民百户家庭人口数的平均数为303.6.
如图是根据我省的统计年鉴中的资料做成的2007年至2016年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到2007年至2016年我省城镇居民百户家庭人口数的平均数为303.6.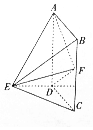 在多面体ABCDE中,ABCD是矩形,平面ABCD⊥平面CDE,CD⊥DE,2DE=2DC=BC,F是棱BC的中点.
在多面体ABCDE中,ABCD是矩形,平面ABCD⊥平面CDE,CD⊥DE,2DE=2DC=BC,F是棱BC的中点.




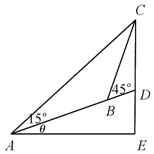 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.求此山对于地平面的倾斜角θ的余弦值.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.求此山对于地平面的倾斜角θ的余弦值.