题目内容
6.已知函数f(x)=xlnx+ax,函数f(x)的图象在点x=1处的切线与直线x+2y-1=0垂直.(1)求a的值和f(x)的单调区间;
(2)求证:ex>f′(x).
分析 (1)由f′(1)=1+a=2,解得:a=1,利用导数求解单调区间.
(2)要证ex>f′(x),即证ex>lnx+2,x>0时,易得ex>x+1,即只需证明x>lnx+1即可
解答 解:(1)f′(x)=lnx+1+a,
f′(1)=1+a=2,解得:a=1,
故f(x)=xlnx+x,f′(x)=lnx+2,
令f′(x)>0,解得:x>e-2,
令f′(x)<0,解得:0<x<e-2,
故f(x)在(0,e-2)递减,在(e-2,+∞)递增;
(2)要证ex>f′(x),即证ex-lnx-2>0,即证ex>lnx+2,
x>0时,易得ex>x+1,即只需证明x+1≥lnx+2即可,
即只需证明x>lnx+1即可
令h(x)=x-lnx+1,则h′(x)=1-$\frac{1}{x}$,
令h′(x)=0,得x=1
h(x)在(0,1)递减,在(1,+∞)递增,
故h(x)≥h(1)=0.
即x+1≥lnx+2成立,即ex>lnx+2,
∴ex>f′(x).
点评 本题考查了导数的综合应用,构造合适的新函数,放缩法证明函数不等式,属于难题.

练习册系列答案
相关题目
16.下列函数中,以π为周期且在区间(0,$\frac{π}{2}$)上为增函数的是( )
| A. | y=sin$\frac{x}{2}$ | B. | y=sin x | C. | y=-tan x | D. | y=-cos 2x |
17.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面A的图形的序号是( )
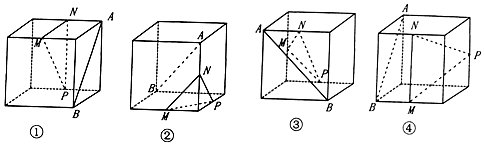

| A. | ①② | B. | ②③ | C. | ①③ | D. | ①③④ |
14.双曲线C的左,右焦点分别为F1(-1,0),F2(1,0),抛物线y2=4x与双曲线C的一个交点为P,若($\overrightarrow{{F}_{2}P}$+$\overrightarrow{{F}_{2}{F}_{1}}$)•($\overrightarrow{{F}_{2}P}$-$\overrightarrow{{F}_{2}{F}_{1}}$)=0,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 1+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
1.执行如图的程序框图,则输出S的值是( )


| A. | log47 | B. | log23 | C. | $\frac{3}{2}$ | D. | 2 |
11.已知复数z满足1+i=(1-i)2z,则z的共轭复数在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天PM2.5日平均浓度(单位:微克/立方米)监测数据,得到甲地PM2.5日平均浓度频率分布直方图和乙地PM2.5日平均浓度的频数分布表.
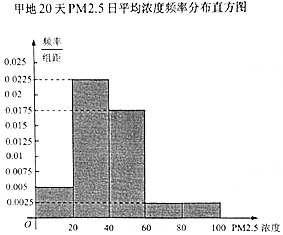
乙地20天PM2.5日平均浓度频数分布表
(1)根据乙地20天PM2.5日平均浓度的频率分布表,作出作出相应的频率分组直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:
从乙地这20天PM2.5日平均浓度不超过40的天数中随机抽取两天,求这两天中至少有一天居民对空气质量满意度为“非常满意”的概率.

乙地20天PM2.5日平均浓度频数分布表
| PM2.5日平均浓度(微克/立方米) | [0,20] | (20,40] | (40,60] | (60,80] | (80,100] |
| 频数(天) | 2 | 3 | 4 | 6 | 5 |
(2)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:
| 满意度等级 | 非常满意 | 满意 | 不满意 |
| PM2.5日平均浓度(微克/立方米) | 不超过20 | 大于20不超过60 | 超过60 |
15.若复数z=2-i+i2,则z2=( )
| A. | 2 | B. | 2i | C. | -2i | D. | $\sqrt{2}$ |