题目内容
11.某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据(x1,y1)(i=1,2,…6)如表所示:| 试销价格x(元) | 4 | 5 | 6 | 7 | a | 9 |
| 产品销量y(件) | b | 84 | 83 | 80 | 75 | 68 |
(1)试判断谁的计算结果正确?并求出a,b的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据“,现从检测数据中随机抽取3个,求“理想数据“的个数ξ的分布列和数学期望.
分析 (1)$\sum_{i=1}^{6}$xi=39,$\sum_{i=1}^{6}$yi=480,x的和为39,y的和为480,解得a和b的值,并求得$\overline{x}$,$\overline{y}$,由x,y具有线性负相关关系,甲同学的不对,将$\overline{x}$,$\overline{y}$,代入验证,乙同学的正确;
(2)分别求出有回归方程求得y值,与实际的y相比较,判断是否为“理想数据“,并求得ξ的取值,分别求得其概率,写出分布列和数学期望.
解答 解:(1)已知变量x,y具有线性负相关关系,故甲不对,
且$\sum_{i=1}^{6}$xi=39,4+5+6+7+a+9=39,a=8,
$\sum_{i=1}^{6}$yi=480,b+84+83+80+75+68=480,b=90,
∵$\overline{x}=\frac{39}{6}$=6.5,
$\overline{y}=\frac{480}{6}$=80,
将$\overline{x}=6.5$,$\overline{y}=80$,代入两个回归方程,验证乙同学正确,
故回归方程为:y=-4x+106;
(2)
| X | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 90 | 84 | 83 | 80 | 75 | 68 |
| y | 92 | 88 | 84 | 80 | 76 | 72 |
P(X=0)=$\frac{1}{{C}_{6}^{3}}$=$\frac{1}{20}$,
P(X=1)=$\frac{{C}_{3}^{1}•{C}_{3}^{2}}{{C}_{6}^{3}}$=$\frac{9}{20}$,
P(X=2)=$\frac{{C}_{3}^{1}{C}_{3}^{2}}{{C}_{6}^{3}}$=$\frac{9}{20}$,
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{6}^{3}}$=$\frac{1}{20}$.
“理想数据“的个数ξ的分布列:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{9}{20}$ | =$\frac{1}{20}$ |
点评 本题考查求回归方程,并结合概率求ξ的分布列和数学期望,在做题过程中要认真审题,确定ξ的取值,属于中档题.

练习册系列答案
相关题目
19.已知定义域为[a-2,2a-1]的奇函数f(x)=x3-sinx+b+1,则f(a)+f(b)的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不能确定 |
11.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{10}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 3 |
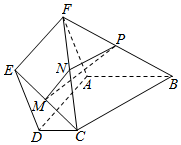 如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.
如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.