题目内容
2.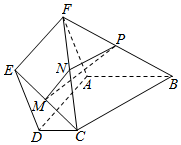 如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.
如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.(Ⅰ)求证:MP∥平面ABCD;
(Ⅱ)求证:平面MNP⊥平面EDC.
分析 (Ⅰ)运用三角形的中位线定理,运用线面平行的判定定理,可得平面MNP∥平面ABCD,再由性质定理即可得证;
(Ⅱ)运用矩形的定义和直角梯形的定义,结合线面垂直的判定定理,可得MN⊥平面ECD,再由面面垂直的判定定理,即可得证.
解答 证明:(Ⅰ)由M,N分别为EC,FC的中点,可得
MN∥EF,又EF∥AD,即有MN∥AD,
MN?平面ABCD,AD?平面ABCD,
可得MN∥平面ABCD;
同理可得NP∥平面ABCD,
又MN∩NP=N,且MN,NP?平面MNP,
可得平面MNP∥平面ABCD,
由MP?平面MNP,
可得MP∥平面ABCD;
(Ⅱ)由矩形ADEF可得AD⊥DE,
由ABCD为直角梯形,且AB⊥AD,
可得AD⊥DC,
即有AD⊥平面ECD,
由AD∥MN,可得MN⊥平面ECD,
由MN?平面MNP,可得
平面MNP⊥平面EDC.
点评 本题考查线面平行的判定,注意运用面面平行的性质定理,考查面面垂直的判定,注意运用判定定理,同时考查线面和面面位置关系的转化思想的运用,考查空间想象能力和逻辑推理的能力,属于中档题.

练习册系列答案
相关题目
12.已知集合A={(x,y)|y=x},B={(x,y)|y=x2},则A∩B为( )
| A. | (0,1) | B. | {0,1} | C. | {(0,1)} | D. | {(0,0),(1,1)} |
13.下列程序运行后,输出的结果是( )


| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
17.已知全集U={1,2,3,4,5,6},集合A={2,4,6},集合B={3,5,6},则A∩(∁UB)=( )
| A. | {2,4,6} | B. | {2,4} | C. | {2,6} | D. | {6} |
11.某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据(x1,y1)(i=1,2,…6)如表所示:
已知变量x,y具有线性负相关关系,且$\sum_{i=1}^{6}$xi=39,$\sum_{i=1}^{6}$yi=480,现有甲、乙、丙三位同学通过计算求得其归直线方程分别为:甲y=4x+54;乙y=-4x+106;丙y=-4.2x+105,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?并求出a,b的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据“,现从检测数据中随机抽取3个,求“理想数据“的个数ξ的分布列和数学期望.
| 试销价格x(元) | 4 | 5 | 6 | 7 | a | 9 |
| 产品销量y(件) | b | 84 | 83 | 80 | 75 | 68 |
(1)试判断谁的计算结果正确?并求出a,b的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据“,现从检测数据中随机抽取3个,求“理想数据“的个数ξ的分布列和数学期望.
 运行如图所示的利程序后,输出的结果为9,7.
运行如图所示的利程序后,输出的结果为9,7.