题目内容
 如图,在三棱柱ABC-A′B′C′中,点E、D分别是B′C′与BC的中点,求证:平面A′EB∥平面ADC′.
如图,在三棱柱ABC-A′B′C′中,点E、D分别是B′C′与BC的中点,求证:平面A′EB∥平面ADC′.考点:平面与平面平行的判定
专题:空间位置关系与距离
分析:先证明A′E∥AD,再证明A′E∥平面AC′D;同理证明BE∥平面AC′D;即证平面A′BE∥平面AC′D.
解答:
证明:如图所示,
连接DE,
∵E、D分别是B′C′与BC的中点,
∴AA′∥DE,AA′=DE,
∴四边形ADEA′是平行四边形;
∴A′E∥AD,
又∵AD?平面AC′D,
A′E?平面AC′D,
∴A′E∥平面AC′D;
又∵EC′=
B′C′,BD=
BC,
且B′C′=BC,B′C′∥BC,
∴EC′∥BD,EC′=BD;
∴四边形BDC′E是平行四边形;
∴BE∥DC′,
又∵BE?平面AC′D,
DC′?平面AC′D,
∴BE∥平面AC′D;
又BE∩A′E=E,BE?平面A′BE,A′E?平面A′BE,
∴平面A′BE∥平面AC′D.

连接DE,
∵E、D分别是B′C′与BC的中点,
∴AA′∥DE,AA′=DE,
∴四边形ADEA′是平行四边形;
∴A′E∥AD,
又∵AD?平面AC′D,
A′E?平面AC′D,
∴A′E∥平面AC′D;
又∵EC′=
| 1 |
| 2 |
| 1 |
| 2 |
且B′C′=BC,B′C′∥BC,
∴EC′∥BD,EC′=BD;
∴四边形BDC′E是平行四边形;
∴BE∥DC′,
又∵BE?平面AC′D,
DC′?平面AC′D,
∴BE∥平面AC′D;
又BE∩A′E=E,BE?平面A′BE,A′E?平面A′BE,
∴平面A′BE∥平面AC′D.
点评:本题考查了证明空间中的平面与平面平行的问题,解题时应用判断定理,先证线面平行,再证面面平行,是基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
函数y=
的定义域是( )
| lg(2-4x) |
A、(0,
| ||
B、(-∞,
| ||
C、(0,
| ||
D、(-∞,
|
 如图,在空间直角坐标系中,BC=4,原点O是BC的中点,点D在平面yOz内,且∠BDC=90°,∠DCB=30°,则点D的坐标为
如图,在空间直角坐标系中,BC=4,原点O是BC的中点,点D在平面yOz内,且∠BDC=90°,∠DCB=30°,则点D的坐标为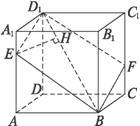 如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.
如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.