题目内容
19.一个几何体的三视图如图所示,则这个几何体的表面积为( )
| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
分析 由三视图还原原几何体,原几何体是一个以正视图为底面的四棱锥,侧面PAB与底面ABCD垂直,底面ABCD是边长为4的正方形,侧面PAB是等腰三角形,底边AB上的高为2,侧面PAD、PBC是全等的直角三角形,直角边AD=4,AP=$2\sqrt{2}$,侧面PCD是等腰三角形,底边CD=4,腰PD=PC=2$\sqrt{6}$.然后由三角形面积求解.
解答 解:由三视图可得原几何体如图: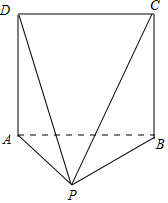
该几何体是一个以正视图为底面的四棱锥,
侧面PAB与底面ABCD垂直,底面ABCD是边长为4的正方形;
侧面PAB是等腰三角形,底边AB上的高为2,侧面PAD、PBC是全等的直角三角形,直角边AD=4,AP=$2\sqrt{2}$;
侧面PCD是等腰三角形,底边CD=4,腰PD=PC=2$\sqrt{6}$.
∴几何体的表面积为:$4×4+\frac{1}{2}×4×2+2×\frac{1}{2}×2\sqrt{2}×4+$$\frac{1}{2}×4×\sqrt{(2\sqrt{6})^{2}-{2}^{2}}$
=20+$8\sqrt{2}$+$4\sqrt{5}$.
故选:B.
点评 本题考查由三视图求几何体的表面积,关键是由三视图还原原几何体,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知f(x)是定义在R上的函数,其导函数f'(x)满足f'(x)<f(x)(x∈R),则( )
| A. | f(2)>e2f(0),f(2001)>e2001f(0) | B. | f(2)<e2f(0),f(2001)>e2001f(0) | ||
| C. | f(2)>e2f(0),f(2001)<e2001f(0) | D. | f(2)<e2f(0),f(2001)<e2001f(0) |
4.函数f(x)=lg(|x|-1)的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
11.设函数$f(x)=-\frac{1}{3}{x}^{3}+x$在(t,10-t2)上有最大值,则实数t的取值范围为( )
| A. | $(-3,-\sqrt{6})$ | B. | $(-2,-\sqrt{3})$ | C. | [-2,1) | D. | (-2,1) |
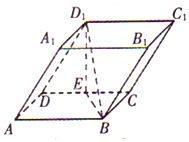 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.