题目内容
6.已知A={(x,y)|x2+y2≤π2},B是曲线y=sinx与x轴围成的封闭区域,若向区域A内随机投入一点M,则点M落入区域B的概率为( )| A. | $\frac{2}{π}$ | B. | $\frac{4}{π}$ | C. | $\frac{2}{{π}^{3}}$ | D. | $\frac{4}{{π}^{3}}$ |
分析 先求构成试验的全部区域为圆内的区域的面积,再利用积分知识可得正弦曲线y=sinx与x轴围成的区域记为M的面积,代入几何概率的计算公式可求.
解答  解:构成试验的全部区域为圆内的区域,面积为π3,正弦曲线y=sinx与x轴围成的区域记为M,
解:构成试验的全部区域为圆内的区域,面积为π3,正弦曲线y=sinx与x轴围成的区域记为M,
根据图形的对称性得:面积为S=2∫0πsinxdx=-2cosx|0π=4,
由几何概率的计算公式可得,随机往圆O内投一个点A,则点A落在区域M内的概率P=$\frac{4}{{π}^{3}}$,
故选:D.
点评 本题主要考查了利用积分求解曲面的面积,几何概率的计算公式的运用,要求熟练掌握函数的积分公式和几何概型的概率公式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
1.二项式($\frac{\sqrt{x}}{2}$-$\frac{2}{x}$)10的展开式中,$\sqrt{x}$项的系数是( )
| A. | $\frac{15}{2}$ | B. | -$\frac{15}{2}$ | C. | 15 | D. | -15 |
18.已知命题“?x∈R,ax2+4x+1>0”是假命题,则实数a的取值范围是( )
| A. | (4,+∞) | B. | (0,4] | C. | (-∞,4] | D. | [0.4) |
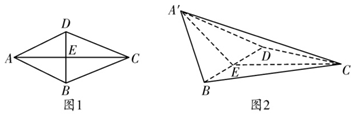
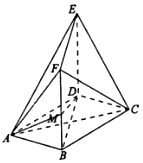 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.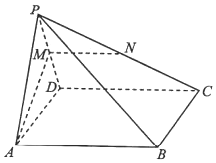 如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证: