题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-1(x≤0)}\\{f(x-1)(x>0)}\end{array}\right.$,若函数g(x)=f(x)-ax+1有5个不同的零点,则实数α的取值范围是[$\frac{1}{5}$,$\frac{1}{4}$).分析 利用函数g(x)=f(x)-ax+1有5个不同的零点,转化为两个函数的图象的交点,画出函数的图象,判断求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-1(x≤0)}\\{f(x-1)(x>0)}\end{array}\right.$,若函数g(x)=f(x)-ax+1有5个不同的零点,
就是y=f(x)与y=ax-1的图象有5个交点,画出函数y=f(x)与y=ax-1的图象如图: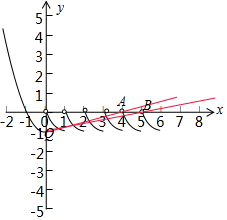
y=ax-1恒过Q(0,-1),直线的斜率为a,满足题目条件,可知kQA>a≥kQB,kQA=$\frac{1}{4}$,kQB=$\frac{1}{5}$,
则实数α的取值范围是:[$\frac{1}{5}$,$\frac{1}{4}$).
给答案为:[$\frac{1}{5}$,$\frac{1}{4}$)
点评 本题考查函数的零点个数的判断,数形结合的应用,考查计算能力.

练习册系列答案
相关题目
5.设i是虚数单位,$\overline{z}$表示复数z的共轭复数,若z=2-i,则z+i$\overline{z}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.已知随机变量ξ服从正态分布N(2,σ2),若P(0≤ξ≤2)=0.3,则P(ξ≥4)=( )
| A. | 0.2 | B. | 0.3 | C. | 0.6 | D. | 0.8 |
6.已知A={(x,y)|x2+y2≤π2},B是曲线y=sinx与x轴围成的封闭区域,若向区域A内随机投入一点M,则点M落入区域B的概率为( )
| A. | $\frac{2}{π}$ | B. | $\frac{4}{π}$ | C. | $\frac{2}{{π}^{3}}$ | D. | $\frac{4}{{π}^{3}}$ |
3.数列{an}满足:a1=-9,an+1-an=2,Sn是其前n项和,则S10=( )
| A. | 0 | B. | -9 | C. | 10 | D. | -10 |
4.下列函数中,值域为[0,+∞)的偶函数是( )
| A. | y=x2-1 | B. | y=|x| | C. | y=lgx | D. | y=cosx |