题目内容
11.已知函数f(x)=x-alnx,当x>1时,f(x)>0恒成立,则实数a的取值范围是( )| A. | (1,+∞) | B. | (-∞,1) | C. | (e,+∞) | D. | (-∞,e) |
分析 由f(x)>0对x∈(1,+∞)上恒成立可分a≤1和a>1来讨论转化为函数的最小值大于等于0的问题来求解.
解答 解:f′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,
当a≤1时,f'(x)≥0在(1,+∞)上恒成立,
则f(x)是单调递增的,
则f(x)>f(1)=1恒成立,则a≤2,
当a>1时,令f′(x)>0,解得:x>a,令f′(x)<0,解得:1<x<a,
故f(x)在(1,a)上单调递减,在(a,+∞)上单调递增,
所以只需f(x)min=f(a)=a-alna>0,解得:a<e,
综上:a<e,
故选:D.
点评 本题考查函数的导数以及利用导数求函数的单调区间和极值问题;考查了利用函数的导数讨论含参数不等式的恒成立问题,求参数的取值范围,主要转化为函数的最值问题利用导数这一工具来求解.

练习册系列答案
相关题目
2.用数学归纳法证明不等$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{11}{24}({n∈{N^*}})$式的过程中,由n=k递推到n=k+1时,下列说法正确的是( )
| A. | 增加了一项$\frac{1}{{2({k+1})}}$ | B. | 增加了两项$\frac{1}{2k+1}$和$\frac{1}{{2({k+1})}}$ | ||
| C. | 增加了B中两项,但又少了一项$\frac{1}{k+1}$ | D. | 增加了A中一项,但又少了一项$\frac{1}{k+1}$ |
6.若x0是方程lnx+x-3=0的实数解,则x0属于区间( )
| A. | (1,1.5) | B. | (1.5,2) | C. | (2,2.5) | D. | (2.5,3) |
20.一个几何体的三视图如图所示,则它的体积为( )
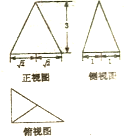

| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
