题目内容
12.在直角坐标系xOy中,曲线C的参数方程为:$\left\{{\begin{array}{l}{x=1+\sqrt{7}cosθ}\\{y=\sqrt{7}sinθ}\end{array}}\right.(θ是参数)$,以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线C的极坐标方程;
(Ⅱ)已知直线l1:$2ρsin(θ+\frac{π}{3})-\sqrt{3}=0$,射线${l_2}:θ=\frac{π}{3}(ρ>0)$与曲线C的交点为P,l2与直线l1的交点为Q,求线段PQ的长.
分析 (Ⅰ)把参数方程消去参数,可得曲线C的普通方程,再根据x=ρcosθ,y=ρsinθ,可得曲线C的极坐标方程.
(Ⅱ)利用极坐标方程求得P、Q的坐标,可得线段PQ的长.
解答 解:(Ⅰ)曲线C的参数方程为:$\left\{{\begin{array}{l}{x=1+\sqrt{7}cosθ}\\{y=\sqrt{7}sinθ}\end{array}}\right.(θ是参数)$,普通方程为(x-1)2+y2=7,
x=ρcosθ,y=ρsinθ代入,可得曲线C的极坐标方程为ρ2-2ρcosθ-6=0;
(Ⅱ)设P(ρ1,θ1),则有$\left\{\begin{array}{l}{{ρ}^{2}-2ρcosθ-6=0}\\{θ=\frac{π}{3}}\end{array}\right.$,解得ρ1=3,θ1=$\frac{π}{3}$,即P(3,$\frac{π}{3}$).
设Q(ρ2,θ2),则有$\left\{\begin{array}{l}{2ρsin(θ+\frac{π}{3})-\sqrt{3}=0}\\{θ=\frac{π}{3}(ρ>0)}\end{array}\right.$,解得ρ2=1,θ2=$\frac{π}{3}$,即Q(1,$\frac{π}{3}$),
所以|PQ|=|ρ1-ρ2|=2.
点评 本题主要考查参数方程与普通方程的互化,极坐标方程的应用以及极坐标的意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.用数学归纳法证明不等$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{11}{24}({n∈{N^*}})$式的过程中,由n=k递推到n=k+1时,下列说法正确的是( )
| A. | 增加了一项$\frac{1}{{2({k+1})}}$ | B. | 增加了两项$\frac{1}{2k+1}$和$\frac{1}{{2({k+1})}}$ | ||
| C. | 增加了B中两项,但又少了一项$\frac{1}{k+1}$ | D. | 增加了A中一项,但又少了一项$\frac{1}{k+1}$ |
20.一个几何体的三视图如图所示,则它的体积为( )
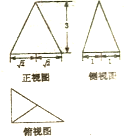

| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
2.不等式$\frac{x+3}{4-x}≥0$的解集为( )
| A. | [-3,4] | B. | [-3,4) | C. | (-∞,-3)∪(3,+∞) | D. | (-∞,-3]∪(4,+∞) |