题目内容
9.a>0是函数y=ax2+x+1在(0,+∞)上单调递增的充分不必要条件.分析 对于函数y=ax2+x+1,对a分类讨论,利用一次函数与二次函数的单调性即可判断出结论.
解答 解:对于函数y=ax2+x+1,a=0时,y=x+1在(0,+∞)上单调递增;
a>0时,y=a$(x+\frac{1}{2a})^{2}$+1-$\frac{1}{4a}$在$(-\frac{1}{2a},+∞)$上单调递增,因此在(0,+∞)上单调递增;
a<0时,y=a$(x+\frac{1}{2a})^{2}$+1-$\frac{1}{4a}$在$(-\frac{1}{2a},+∞)$上单调递减,因此在(0,+∞)上单调递减.
由以上可得:a>0是函数y=ax2+x+1在(0,+∞)上单调递增的充分不必要条件.
故答案为:充分不必要.
点评 本题考查了函数的单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.一个几何体的三视图如图所示,则它的体积为( )
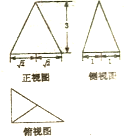

| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
14.命题p:“?x∈N+,($\frac{1}{2}$)x≤$\frac{1}{2}$”的否定为( )
| A. | ?x∈N+,($\frac{1}{2}$)x>$\frac{1}{2}$ | B. | ?x∉N+,($\frac{1}{2}$)x>$\frac{1}{2}$ | C. | ?x∉N+,($\frac{1}{2}$)x>$\frac{1}{2}$ | D. | ?x∈N+,($\frac{1}{2}$)x>$\frac{1}{2}$ |
18.已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>-2f(x),若g(x)=x2f(x),则不等式g(x)<g(1)的解集是( )
| A. | (-∞,1) | B. | (-∞,0)∪(0,1) | C. | (-1,1) | D. | (-1,0)∪(0,1) |
5.若sinθ•cosθ>0,sinθ+cosθ<0,则tanθ-cosθ的值( )
| A. | 恒为正数 | B. | 恒为负数 | C. | 恒为非正数 | D. | 恒为非负数 |