题目内容
10．已知数列{an}为等比数列，Sn为其前n项和，且${S_n}=2017×{2016^n}-2018t$，则t=（ ）| A． | $\frac{2015}{2016}$ | B． | $\frac{2016}{2017}$ | C． | $\frac{2017}{2018}$ | D． | $\frac{2018}{2019}$ |
分析 先分别求出a1，a2，a3，由等比数列{an}中，${{a}_{2}}^{2}={a}_{1}{a}_{3}$，能求出t的值．
解答 解：∵数列{an}为等比数列，Sn为其前n项和，且${S_n}=2017×{2016^n}-2018t$，
∴a1=S1=2017×2016-2018t，
a2=S2-S1=（2017×20162-2018t）-（2017×2016-2018t）=2017×2016×2015，
a3=S3-S2=（2017×20162-2018t）-（2017×20162-2018t）=2017×20162×2015，
∵等比数列{an}中，${{a}_{2}}^{2}={a}_{1}{a}_{3}$，
∴（2017×2016×2015）2=（2017×2016-2018t）×（2017×20162×2015），
解得t=$\frac{2017}{2018}$．
故选：C．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
20．一个几何体的三视图如图所示，则它的体积为（ ）
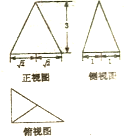
| A． | $2\sqrt{2}$ | B． | $2\sqrt{3}$ | C． | $6\sqrt{2}$ | D． | $6\sqrt{3}$ |
18．已知定义域为{x|x≠0}的偶函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞-2f（x），若g（x）=x2f（x），则不等式g（x）＜g（1）的解集是（ ）
| A． | （-∞，1） | B． | （-∞，0）∪（0，1） | C． | （-1，1） | D． | （-1，0）∪（0，1） |
2．不等式$\frac{x+3}{4-x}≥0$的解集为（ ）
| A． | [-3，4] | B． | [-3，4） | C． | （-∞，-3）∪（3，+∞） | D． | （-∞，-3]∪（4，+∞） |
5．若sinθ•cosθ＞0，sinθ+cosθ＜0，则tanθ-cosθ的值（ ）
| A． | 恒为正数 | B． | 恒为负数 | C． | 恒为非正数 | D． | 恒为非负数 |