题目内容
6.已知函数f(x)=|x-3|+|x-1|,若存在x∈R,使f(x)≥2a,则实数a的取值范围是(-∞,1].分析 根据绝对值的性质求出f(x)的最小值,从而求出a的范围即可.
解答 解:∵f(x)=|x-3|+|x-1|≥|x-3-x+1|=2,
故2a≤2,解得:a≤1,
故答案为:(-∞,1].
点评 本题考查了绝对值的性质,考查函数最值问题,是一道基础题.

练习册系列答案
相关题目
16.设全集U={1,2,3,4,5},集合A={1,2},B={x|x2-5x+6=0},则A∩(∁UB)=( )
| A. | {4,5} | B. | {2,3} | C. | {1} | D. | {4} |
1.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且$\frac{{S}_{1}}{{S}_{2}}$=$\frac{16}{9}$,则$\frac{{V}_{1}}{{V}_{2}}$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
16.一个底面是正三角形的三棱柱的正视图如图所示,则其体积等于( )
 .
.
 .
.| A. | 2$\sqrt{3}$ | B. | 4$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
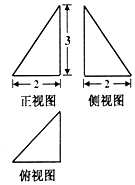 已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.
已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2. 如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.
如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.