题目内容
曲线y=ln(2x-1)-5上的点到直线2x-y+3=0的最短距离为( )
A、
| ||
B、2
| ||
C、3
| ||
| D、0 |
考点:点到直线的距离公式
专题:直线与圆
分析:先求出:直线与直线2x-y+3=0平行且与曲线y=ln(2x-1)-5相切的切点,再利用点到直线的距离公式即可得出.
解答:
解:设直线与直线2x-y+3=0平行且与曲线y=ln(2x-1)-5相切的切点为P(x,y).
y′=
,令y′=2,解得x=1,∴y=-5,∴P(1,-5).
点P到直线2x-y+3=0的距离d=
=2
.
∴曲线y=ln(2x-1)-5上的点到直线2x-y+3=0的最短距离d=2
.
故选:B.
y′=
| 2 |
| 2x-1 |
点P到直线2x-y+3=0的距离d=
| |2×1-(-5)+3| | ||
|
| 5 |
∴曲线y=ln(2x-1)-5上的点到直线2x-y+3=0的最短距离d=2
| 5 |
故选:B.
点评:本题考查了导数的几何意义、点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
函数f(x)=x2-3x+2的零点是( )
| A、(1,0),(2,0) |
| B、(0,1),(0,2) |
| C、1,2 |
| D、-1,-2 |
过点A(3,3)与双曲线C:
-
=1有且仅有一个交点的直线有( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、1条 | B、2条 | C、3条 | D、4条 |
数列
,
,
,
,
,
,…,
,
,…,
,…的前40项的和是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 1 |
| m+1 |
| 2 |
| m+1 |
| m |
| m+1 |
A、23
| ||
B、19
| ||
| C、19 | ||
| D、18 |
已知复数z=
,则z的虚部为( )
| ||
1-
|
| A、i | B、-i | C、1 | D、0 |
等差数列{an}中,a5+a9-a7=10,则S13的值为( )
| A、130 | B、260 |
| C、156 | D、168 |
函数f(x)=x2+2(a-1)x+2在区间(-∞,3]上单调递减,那么实数a的取值范围是( )
| A、a≤-2 | B、a≥-2 |
| C、a≤4 | D、a≥4 |
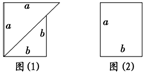 如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为
如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为