题目内容
已知向量
=(2,4)与向量
=(-4,y)垂直,则y=( )
| a |
| b |
| A、-2 | B、-1 | C、1 | D、2 |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:根据两个向量垂直可得
•
=0,再利用向量的坐标表示出两个向量的数量积,进而得到关于y的方程并且求出y的数值.
| a |
| b |
解答:
解:因为平面向量
=(2,4)与向量
=(-4,y)垂直,
所以
•
=0,即2×(-4)+4×y=0,解得:y=2.
故选:D.
| a |
| b |
所以
| a |
| b |
故选:D.
点评:本题主要考查向量的数量积运算及向量垂直的充要条件,本题属于基础题只要计算正确即可得到全分.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
下列函数既是奇函数,又在区间(-1,1)内是减函数的是( )
| A、f(x)=-|x| |
| B、f(x)=lg(1-x)-lg(1+x) |
| C、f(x)=2x+2-x |
| D、f(x)=-x3sin2x |
已知sinθ-cosθ=
,则sin2θ的值是( )
| 1 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
某汽车生产厂家准备推出10款不同的轿车参加车展,但主办方只能为该厂提供6个展位,每个展位摆放一辆车,并且甲、乙两款车不能摆放在1号展位,那么该厂家参展轿车的不同摆放方案有( )
A、C
| ||||
B、C
| ||||
C、C
| ||||
D、C
|
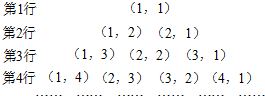 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.