题目内容
12.已知A(1,2,-1),B(5,6,7),则直线AB与平面xoz交点的坐标是( )| A. | (0,1,1) | B. | (0,1,-3) | C. | (-1,0,3) | D. | (-1,0,-5) |
分析 设出直线AB与平面xoz交点的坐标M(x,0,z),根据向量$\overrightarrow{AM}$与$\overrightarrow{AB}$共线,列出方程组求出x、z的值.
解答 解:直线AB与平面xoz交点的坐标是M(x,0,z),
则$\overrightarrow{AM}$=(x-1,-2,z+1),$\overrightarrow{AB}$=(4,4,8);
又$\overrightarrow{AM}$与$\overrightarrow{AB}$共线,
∴$\overrightarrow{AM}$=λ$\overrightarrow{AB}$;
即$\left\{\begin{array}{l}{x-1=4λ}\\{-2=4λ}\\{z+1=8λ}\end{array}\right.$,
解得x=-1,z=-5;
∴点M(-1,0,-5).
故选:D.
点评 本题考查了空间向量的坐标表示与共线定理的应用问题,是基础题目.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{5}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
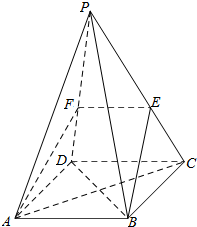 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.