题目内容
16.函数f(x)=sinx•(4cos2x-1)的最小正周期是( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
分析 利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期.
解答 解:函数f(x)=sinx•(4cos2x-1)
化简可得:f(x)=4sinx•cos2x-sinx=4sinx(1-sin2x)-sinx=3sinx-4sin3x=sin3x.
∴最小正周期T=$\frac{2π}{3}$.
故选:B.
点评 本题考查了二倍角和两角和与差公式的化解能力和计算能力.属于中档题.

练习册系列答案
相关题目
13.已知复数z=$\frac{2i}{1+i}$,则z•$\overline z$=( )
| A. | 2 | B. | 2i | C. | 4 | D. | 4i |
1.已知$cosα-sinα=\frac{{\sqrt{2}}}{4}$,则sin2α的值为( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{7}{8}$ | D. | $-\frac{7}{8}$ |
8.若a,b∈R,ab≠0,且a+b=1,则下列不等式中,恒成立的是( )
| A. | a2b2≤$\frac{1}{16}$ | B. | a2+b2≥$\frac{1}{2}$ | C. | (1+$\frac{1}{a}$)(1+$\frac{1}{b}$)≥9 | D. | $\frac{1}{a}$+$\frac{1}{b}$≥4 |
6.若双曲线M:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点分别是F1,F2,以F1F2为直径的圆与双曲线M相交于点P,且|PF1|=16,|PF2|=12,则双曲线M的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 5 |
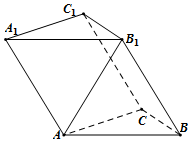 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.