题目内容
8.若a,b∈R,ab≠0,且a+b=1,则下列不等式中,恒成立的是( )| A. | a2b2≤$\frac{1}{16}$ | B. | a2+b2≥$\frac{1}{2}$ | C. | (1+$\frac{1}{a}$)(1+$\frac{1}{b}$)≥9 | D. | $\frac{1}{a}$+$\frac{1}{b}$≥4 |
分析 由a,b∈R,ab≠0,且a+b=1,恒大于0,两边平方,根据不等式的性质可得答案.
解答 解:由a+b=1,可得a2+b2+2ab=1,
∵2ab≤a2+b2,当且仅当a=b时取等号.
∴2a2+2b2≥1,
则a2+b2≥$\frac{1}{2}$.
故选B.
点评 本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
4.将长宽分别为2和1的长方形ABCD沿对角线AC折起,得到四面体A-BCD,则四面体A-BCD外接球的表面积为( )
| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
16.函数f(x)=sinx•(4cos2x-1)的最小正周期是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
13.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,若在曲线C的右支上存在点P,使得△PF1F2的内切圆半径为a,圆心记为M,又△PF1F2的重心为G,满足MG平行于x轴,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
18.已知函数$f(x)=\left\{\begin{array}{l}2-{log_2}(-x+2),0≤x<2\\ 2-f(-x),-2<x<0\end{array}\right.$则|f(x)|≤2的解集为( )
| A. | [0,1] | B. | (-2,1] | C. | $[-\frac{7}{4},2)$ | D. | $[{-\frac{7}{4},1}]$ |
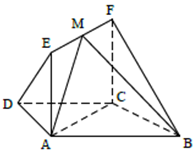 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.