题目内容
5.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足bcosC+(2a+c)cosB=0.(I)求角B的值;
(II)若b=1,$cosA+cosC=\sqrt{3}$,求△ABC的面积.
分析 (I)利用正弦定理化简bcosC+(2a+c)cosB=0可得角B的值;
(II)根据三角内角和定理,消去C角,利用和与差公式以及同角三角函数关系式求出A,C.即可求出△ABC的面积.
解答 解:(I)∵bcosC+(2a+c)cosB=0.
由正弦定理sinBcosC+2sinAcosB+sinCcosB=0,即sinA+2sinAcosB=0,
∵sinA≠0
∴cosB=$-\frac{1}{2}$,
∵0<B<π,
∴B=$\frac{2π}{3}$.
(II)由(I)可得B=$\frac{2π}{3}$.
那么C=60°-A.
∵$cosA+cosC=\sqrt{3}$,
即cosA+cos60°cosA+sin60°sinA=$\sqrt{3}$;
?$\frac{3}{2}cosA+\frac{\sqrt{3}}{2}sinA=\sqrt{3}$.
?$\sqrt{3}$sin(A+$\frac{π}{3}$)=$\sqrt{3}$
∴sin(A+$\frac{π}{3}$)=1.
∴A=$\frac{π}{6}$,
∴C=$\frac{π}{6}$.
∴△ABC是等腰三角形.
故得△ABC的面积S=$\frac{1}{2}$×1×$\frac{1}{2}$×tan$\frac{π}{6}$=$\frac{\sqrt{3}}{12}$.
点评 本题考查了正弦定理,三角内角和定理的化解能力和计算能力.属于基础题.

练习册系列答案
相关题目
16.函数f(x)=sinx•(4cos2x-1)的最小正周期是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
13.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,若在曲线C的右支上存在点P,使得△PF1F2的内切圆半径为a,圆心记为M,又△PF1F2的重心为G,满足MG平行于x轴,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
10.如果复数$\frac{2-ai}{1+i}$(其中i为虚数单位,a∈R)为纯虚数,则a=( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
14.A={x|y=lg(x2+3x-4)},$B=\left\{{y\left|{y={2^{1-{x^2}}}}\right.}\right\}$,则A∩B=( )
| A. | (0,2] | B. | (1,2] | C. | [2,4) | D. | (-4,0) |
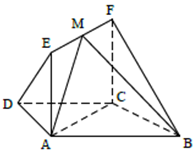 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.