题目内容
13．已知复数z=$\frac{2i}{1+i}$，则z•$\overline z$=（ ）| A． | 2 | B． | 2i | C． | 4 | D． | 4i |
分析 利用复数的运算法则、共轭复数的定义即可得出．
解答 解：复数z=$\frac{2i}{1+i}$=$\frac{2i（1-i）}{（1+i）（1-i）}$=i+1，则z•$\overline z$=（1+i）（1-i）=2．
故选：A．
点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
3．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（x+2），}&{x≥2}\\{{2}^{1-x}，}&{x＜2}\end{array}\right.$（a＞0且a≠1），若f（6）+f（-1）=7，函数y=f（x）-b仅有一个零点，则实数b的取值范围为（ ）
| A． | [$\frac{1}{2}$，2] | B． | （$\frac{1}{2}$，2] | C． | [$\frac{1}{2}$，2） | D． | （$\frac{1}{2}$，2） |
4．将长宽分别为2和1的长方形ABCD沿对角线AC折起，得到四面体A-BCD，则四面体A-BCD外接球的表面积为（ ）
| A． | 3π | B． | 5π | C． | 10π | D． | 20π |
8．已知函数f（x）=sin（x+φ）-$\sqrt{3}$cos（x+φ）（|φ|＜$\frac{π}{2}$）的图象关于直线x=π对称，则cos2φ=（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
18．已知抛物线C：y2=2px（p＞0）的焦点为F，点Q（0，$\sqrt{3}$），射线FQ与C交于点E，与C的准线交于点P，且$\overrightarrow{PE}=2\overrightarrow{EF}$，则点E到y轴的距离是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | 1 |
16．函数f（x）=sinx•（4cos2x-1）的最小正周期是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | π | D． | 2π |
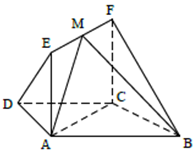如图，在等腰梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，$CF=\sqrt{2}$．