题目内容
已知函数f(x)=loga
(a>1)为奇函数
(1)求实数m的值;
(2)指出函数y=f(x)的单调区间(无需证明);
(3)若仅有一个常数c使得对于任意的s∈[a,2014a],都有t∈[a,a2]满足方程f(
)+f(
)=c,求实数a的值.
| mx+1 |
| x-1 |
(1)求实数m的值;
(2)指出函数y=f(x)的单调区间(无需证明);
(3)若仅有一个常数c使得对于任意的s∈[a,2014a],都有t∈[a,a2]满足方程f(
| s+1 |
| s-1 |
| t+1 |
| t-1 |
考点:函数单调性的判断与证明,函数奇偶性的性质
专题:转化思想,函数的性质及应用
分析:(1)由函数f(x)是奇函数,得f(-x)+f(x)=0,求出m的值;
(2)m=1时,f(x)=loga
,求出f(x)的单调区间;
(3)由题意,f(
)+f(
)=c可化为logas+logat=c,即s=
(a>1);
考查反比例函数s=
在区间[a,a2]的单调性,得
,从而求出a、c的值.
(2)m=1时,f(x)=loga
| x+1 |
| x-1 |
(3)由题意,f(
| s+1 |
| s-1 |
| t+1 |
| t-1 |
| ac |
| t |
考查反比例函数s=
| ac |
| t |
|
解答:
解:(1)∵函数f(x)=loga
(a>1)为奇函数,
∴f(-x)+f(x)=loga
+loga
=loga
=0,
∴1-m2x2=1-x2,
即m=±1,m=-1不合题意,
∴m=1;
(2)当m=1时,奇函数f(x)=loga
,
>0;
∴x<-1,或x>1;
∴f(x)的单调区间是(-∞,-1)和(1,+∞);
(3)∵f(
)+f(
)=c,即logas+logat=c;
∴s>0,t>0,∴s=
(a>1);
该函数是反比例函数,
∴函数s=
在区间[a,a2]上单调递减;
∴
,
又∵a>1,c只有一个值;
∴解得c=3,a=2014,
即实数a的值是2014.
| mx+1 |
| x-1 |
∴f(-x)+f(x)=loga
| -mx+1 |
| -x-1 |
| mx+1 |
| x-1 |
=loga
| (-mx+1)(mx+1) |
| (-x-1)(x-1) |
∴1-m2x2=1-x2,
即m=±1,m=-1不合题意,
∴m=1;
(2)当m=1时,奇函数f(x)=loga
| x+1 |
| x-1 |
| x+1 |
| x-1 |
∴x<-1,或x>1;
∴f(x)的单调区间是(-∞,-1)和(1,+∞);
(3)∵f(
| s+1 |
| s-1 |
| t+1 |
| t-1 |
∴s>0,t>0,∴s=
| ac |
| t |
该函数是反比例函数,
∴函数s=
| ac |
| t |
∴
|
又∵a>1,c只有一个值;
∴解得c=3,a=2014,
即实数a的值是2014.
点评:本题考查了函数的性质与应用问题,解题时应用转化思想,利用函数的单调性求方程组的解,是中档题.

练习册系列答案
相关题目
在△ABC中,
=
,
=
,且
=
,则
=( )

| AB |
| a |
| AC |
| b |
| BD |
| 1 |
| 2 |
| DC |
| AD |

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列命题中,真命题是( )
A、存在x0∈R,sin2
| ||||||
| B、任意x∈(0,π),sinx>cosx | ||||||
| C、任意x∈(0,+∞),x2+1>x | ||||||
| D、存在x0∈R,x02+x0=-1 |
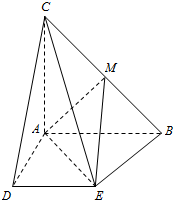 在△ABC中,AB=AC,∠CAB=90°,且
在△ABC中,AB=AC,∠CAB=90°,且