题目内容
8.在△ABC中,∠A=60°,$a=\sqrt{6}$,$b=\sqrt{2}$,则△ABC解的情况( )| A. | 无解 | B. | 有唯一解 | C. | 有两解 | D. | 不能确定 |
分析 根据正弦定理,结合题中数据解出sinB,再由∠B+∠C=180°-∠A=120°,得出B<120°,所以∠B=30°,从而∠C=90°.由此可得满足条件的△ABC有且只有一个.
解答  解:∵△ABC中,∠A=60°,a=$\sqrt{6}$,b=$\sqrt{2}$,
解:∵△ABC中,∠A=60°,a=$\sqrt{6}$,b=$\sqrt{2}$,
∴根据正弦定理,得sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{6}}$=$\frac{1}{2}$,
∵∠A=60°,得∠B+∠C=120°
∴由sinB=$\frac{1}{2}$,得∠B=30°,从而得到∠C=90°
因此,满足条件的△ABC有且只有一个.
故选:B.
点评 本题给出三角形ABC的两条边的一个角,求满足条件的三角形个数.着重考查了利用正弦定理解三角形的知识,属于基础题.

练习册系列答案
相关题目
18.已知圆C:x2+y2=9,直线l1:x-y-1=0与l2:x+2y-10=0的交点设为P点,过点P向圆C作两条切线a,b分别与圆相切于A,B两点,则S△ABP=$\frac{192}{25}$.
19.如果二次函数y=x2+4x+(m+3)有两个不同的零点,则m的取值范围是( )
| A. | (-∞,1) | B. | (-2,6) | C. | [-2,6] | D. | {-2,6} |
16.函数$f(x)=\left\{\begin{array}{l}2x-{x^2},0≤x≤3\\{x^2}+6x,-2≤x<0\end{array}\right.$的值域是( )
| A. | [-8,1] | B. | [-8,-3] | C. | R | D. | [-9,1] |
3.下列不等式中,解集是空集的是( )
| A. | x2-x+1>0 | B. | 2x-x2>5 | C. | -2x2+x+1>0 | D. | x2+x>2 |
13.直线l:x+y+1=0的倾斜角为( )
| A. | 45° | B. | 135° | C. | 1 | D. | -1 |
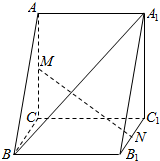 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.