题目内容
18.已知数列{an}的前n项和${S_n}={n^2}$,等比数列{bn},b1=a1,b4是a4与a5的等差中项.(1)求数列{an},{bn}的通项公式;
(2)记cn=an•bn,求数列{cn}的前n项和Tn.
分析 (1)求出数列{an}的首项a1,利用n≥2,${a_n}={S_n}-{S_{n-1}}={n^2}-{(n-1)^2}=2n-1$,求出通项公式,然后求解${b_n}={2^{n-1}}$.
(2)化简cn=an•bn,利用错位相减法求解数列的{cn}的前n项和Tn.
解答 解:(1)数列{an}的前n项和${S_n}={n^2}$,所以a1=S1=1…(1分)
n≥2,${a_n}={S_n}-{S_{n-1}}={n^2}-{(n-1)^2}=2n-1$…(2分)
当n=1,也满足an=2n-1…(3分)
所以${a_n}=2n-1,n∈{N^*}$…(4分)
b1=a1=1,2b4=a4+a5=7+9,所以b4=8,…(6分)
${b_4}={b_1}•{q^3}=8$,所以q=2,所以${b_n}={2^{n-1}}$…(7分)
(2)${c_n}={a_n}•{b_n}=(2n-1)•{2^{n-1}}$,
${T_n}=1•{2^0}+3•{2^1}+5•{2^2}+…+(2n-1)•{2^{n-1}}$①…(8分)
$2{T_n}=1•{2^1}+3•{2^2}+5•{2^3}+…+(2n-1)•{2^n}$②…(9分)
①式减去②式得:$-{T_n}=1•{2^0}+2•{2^1}+2•{2^2}+2•{2^3}+…+2•{2^{n-1}}-(2n-1)•{2^n}$…(10分)
$-{T_n}=1+\frac{{{2^2}(1-{2^{n-1}})}}{1-2}-(2n-1)•{2^n}$=-3-(2n-3)•2n…(11分)
∴${T_n}=3+(2n-3)•{2^n}$…(12分)
点评 本题考查数列通项公式,以及数列求和的基本方法,考查计算能力.

练习册系列答案
相关题目
8.在△ABC中,∠A=60°,$a=\sqrt{6}$,$b=\sqrt{2}$,则△ABC解的情况( )
| A. | 无解 | B. | 有唯一解 | C. | 有两解 | D. | 不能确定 |
13.已知等差数列{an}的前n项的和为Sn,若a5+a6=10,则S10=( )
| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
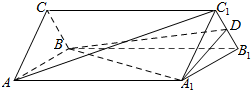 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.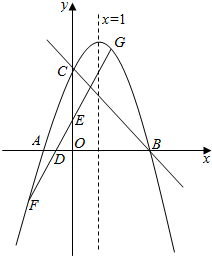 如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.
如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.