题目内容
17.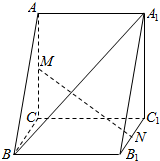 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
分析 (Ⅰ)取AB中点D,连接DM,DB1,然后由三角形的中位线定理得到MN∥DB1,再由线面平行的判定定理得答案;
(Ⅱ)连接BC1,可证QN⊥BC1,A1C1⊥QN,从而可证:A1B⊥QN,同理可得 A1B⊥MQ,即可得证A1B⊥平面MNQ.
解答 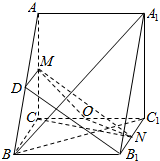 (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)证明:取AB中点D,连接DM,DB1.
在△ABC中,因为 M为AC中点,所以DM∥BC,$DM=\frac{1}{2}BC$.
在矩形B1BCC1中,因为 N为B1C1中点,所以B1N∥BC,${B_1}N=\frac{1}{2}BC$.
所以 DM∥B1N,DM=BN.
所以 四边形MDB1N为平行四边形,所以 MN∥DB1.…(4分)
因为 MN?平面ABB1A1,DB1?平面ABB1A1,
所以 MN∥平面ABB1A1. …(6分)
(Ⅱ)解:线段CC1上存在点Q,且Q为CC1中点时,
有A1B⊥平面MNQ. …(8分)
证明如下:连接BC1.
在正方形BB1C1C中易证 QN⊥BC1.
又A1C1⊥平面BB1C1C,所以 A1C1⊥QN,从而NQ⊥平面A1BC1.
所以 A1B⊥QN. …(10分)
同理可得 A1B⊥MQ,所以A1B⊥平面MNQ.
故线段CC1上存在点Q,使得A1B⊥平面MNQ. …(12分)
点评 本小题主要考查空间线面关系,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在△ABC中,∠A=60°,$a=\sqrt{6}$,$b=\sqrt{2}$,则△ABC解的情况( )
| A. | 无解 | B. | 有唯一解 | C. | 有两解 | D. | 不能确定 |
2.已知命题p:“若直线a与平面α内两条直线垂直,则直线a与平面α垂直”,命题q:“存在两个相交平面垂直于同一条直线”,则下列命题中的真命题为( )
| A. | p∧q | B. | p∨q | C. | ¬p∨q | D. | p∧¬q |
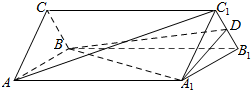 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.