题目内容
16．函数$f（x）=\left\{\begin{array}{l}2x-{x^2}，0≤x≤3\\{x^2}+6x，-2≤x＜0\end{array}\right.$的值域是（ ）| A． | [-8，1] | B． | [-8，-3] | C． | R | D． | [-9，1] |
分析 利用二次函数的性质求解分段函数的值域即可．
解答 解：x∈[0，3]，f（x）=2x-x2，的对称轴为：x=1，开口向下，最大值为：1，最小值为：-3．
x∈[-2，0），f（x）=6x+x2，的对称轴为：x=-3，开口向上，最大值为：0，最小值为：-8．
函数$f（x）=\left\{\begin{array}{l}2x-{x^2}，0≤x≤3\\{x^2}+6x，-2≤x＜0\end{array}\right.$的值域是：[-8，1]．
故选：A．
点评 本题考查分段函数的应用，二次函数的性质的应用，考查计算能力．
练习册系列答案
相关题目
6．已知p：0＜a＜4，q：函数y=x2-ax+a的值恒为正，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
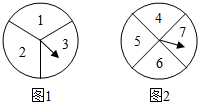某校高一年级甲、已两班准备联合举行晚会，两班各派一人先进行转盘游戏，胜者获得一件奖品，负者表演一个节目．甲班的文娱委员利用分别标有数字1，2，3，4，5，6，7的两个转盘（如图所示），设计了一种游戏方案：两人同时各转动一个转盘一次，将转到的数字相加，和为偶数时甲班代表获胜，否则乙班代表获胜．
8．在△ABC中，∠A=60°，$a=\sqrt{6}$，$b=\sqrt{2}$，则△ABC解的情况（ ）
| A． | 无解 | B． | 有唯一解 | C． | 有两解 | D． | 不能确定 |