题目内容
P为双曲线
-
=1上一点,F1、F2是它的两个焦点,当∠F1PF2为钝角时,点P的纵坐标的取值范围是 .
| x2 |
| 9 |
| y2 |
| 16 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设P(x,y),根据双曲线方程求得两焦点坐标,根据∠F1PF2是钝角推断出推断出
•
<0且y≠0,求得x和y的不等式关系,求得y的范围.
| PF1 |
| PF2 |
解答:
解:设P(x,y),则
∵F1(-5,0),F2(5,0),
∴
=(-5-x,-y),
=(5-x,-y),
∴
•
=(-5-x,-y)•(5-x,-y)=x2+y2-25=
y2-9,
∵∠F1PF2为钝角,
∴
y2-9<0且y≠0,
∴-
<y<
且y≠0.
故答案为:-
<y<
且y≠0.
∵F1(-5,0),F2(5,0),
∴
| PF1 |
| PF2 |
∴
| PF1 |
| PF2 |
| 25 |
| 16 |
∵∠F1PF2为钝角,
∴
| 25 |
| 16 |
∴-
| 12 |
| 5 |
| 12 |
| 5 |
故答案为:-
| 12 |
| 5 |
| 12 |
| 5 |
点评:本题主要考查了双曲线的简单性质和解不等式,∠F1PF2是钝角推断出
•
<0,是解题关键,属中档题.
| PF1 |
| PF2 |

练习册系列答案
相关题目
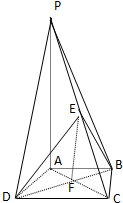 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.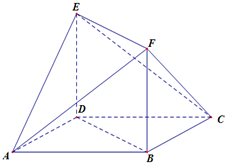 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,