题目内容
已知椭圆的焦点在x轴上,一个顶点为A(0,-1),其右焦点到直线x-y+2
=0的距离为3,则椭圆的方程为 .
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件设椭圆方程为
+y2=1,(a>1),由右焦点到直线x-y+2
=0的距离为3,利用点到直线的距离公式求出a2,由此能求出椭圆方程.
| x2 |
| a2 |
| 2 |
解答:
解:∵椭圆的焦点在x轴上,一个顶点为A(0,-1),
∴设椭圆方程为
+y2=1,(a>1)
∴椭圆的右焦点F(
,0),
∵右焦点到直线x-y+2
=0的距离为3,
∴
=3,
解得a2=3,
∴椭圆方程为
+y2=1.
故答案为:
+y2=1.
∴设椭圆方程为
| x2 |
| a2 |
∴椭圆的右焦点F(
| a2-1 |
∵右焦点到直线x-y+2
| 2 |
∴
|
| ||||
|
解得a2=3,
∴椭圆方程为
| x2 |
| 3 |
故答案为:
| x2 |
| 3 |
点评:本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
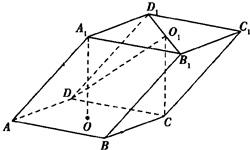 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.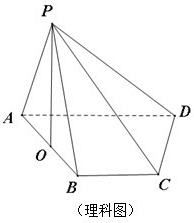 (理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.
(理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.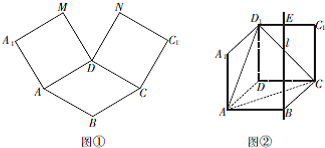 如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).
如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).