题目内容
已知直线l1:5x-2y+3m(3m+1)=0和直线l2:2x+6y-3m(9m+20)=0,求:
(1)两直线l1、l2交点的轨迹方程;
(2)m取何值时,直线l1与l2的交点到直线4x-3y-12=0的距离最短,最短距离是多少?
(1)两直线l1、l2交点的轨迹方程;
(2)m取何值时,直线l1与l2的交点到直线4x-3y-12=0的距离最短,最短距离是多少?
考点:轨迹方程,点到直线的距离公式
专题:直线与圆
分析:(1)由l1、l2的方程组成方程组,解得交点的参数方程,消参数可得交点轨迹的普通方程;
(2)由点到直线的距离公式求出交点到直线4x-3y-12=0的距离d,则d是参数m的函数,利用配方法求最值.
(2)由点到直线的距离公式求出交点到直线4x-3y-12=0的距离d,则d是参数m的函数,利用配方法求最值.
解答:
解:(1)联立
,
①×3+②得,17x=51m,解得x=3m,代入①得,y=
m2+9m.
∴两直线l1、l2交点的轨迹方程为
.
消去参数m得,y=
x2+3x,
∴两直线l1、l2交点的轨迹方程为y=
x2+3x;
(2)设两直线交点到直线4x-3y-12=0的距离为d,
则d=
=
|9m2+10m+8|
=
|(m+
)2+
|,
∴当m=-
时,距离d有最小值为:
×
=
.
|
①×3+②得,17x=51m,解得x=3m,代入①得,y=
| 9 |
| 2 |
∴两直线l1、l2交点的轨迹方程为
|
消去参数m得,y=
| 1 |
| 2 |
∴两直线l1、l2交点的轨迹方程为y=
| 1 |
| 2 |
(2)设两直线交点到直线4x-3y-12=0的距离为d,
则d=
|4•3m-3•(
| ||
|
=
| 3 |
| 10 |
=
| 27 |
| 10 |
| 5 |
| 9 |
| 47 |
| 81 |
∴当m=-
| 5 |
| 9 |
| 27 |
| 10 |
| 47 |
| 81 |
| 47 |
| 30 |
点评:本题考查了利用消参数法求曲线的轨迹方程,考查了点到直线的距离公式,训练了利用配方法求函数的最值,是中档题.

练习册系列答案
相关题目
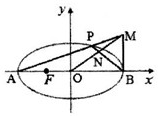 已知椭圆
已知椭圆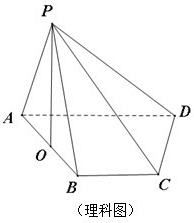 (理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.
(理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.