题目内容
12. 设函数f(x)=log2(x-a)(a∈R).
设函数f(x)=log2(x-a)(a∈R).(1)当a=2时,解方程f(x)-f(x+1)=-1;
(2)如图所示的平面直角坐标系中,每一个小方格的边长均为1,当a=1时,试在该坐标系中作出函数y=|f(x)|的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间.
分析 (1)当a=2,根据对数方程的性质解方程即可得到结论.
(2)根据对数函数的性质,结合对数函数的性质进行求解即可.
解答 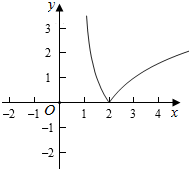 解:(1)当a=2时,f(x)=log2(x-2),
解:(1)当a=2时,f(x)=log2(x-2),
则方程f(x)-f(x+1)=-1等价为log2(x-2)-log2(x-1)=-1,
即1+log2(x-2)=log2(x-1),
即log22(x-2)=log2(x-1),
则2(x-2)=x-1,即x=3,此时log2(3-2)-log2(3-1)=0-1=-1,方程成立.
即方程的解集为{3}.
(2)当a=1时,f(x)=log2(x-1),
则y=|log2(x-1)|=$\left\{\begin{array}{l}{lo{g}_{2}(x-1),}&{x≥2}\\{-lo{g}_{2}(x-1),}&{1<x<2}\end{array}\right.$,
则对应的图形为,
则函数的定义域为(1,+∞),
函数的值域为[0,+∞),
函数为非奇非偶函数,
函数的单调递减区间为为(1,2),函数的单调递增区间为[2,+∞).
点评 本题主要考查对数方程和对数函数的图象和性质的考查,比较基础.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤3}\\{f(6-x),3<x<6}\end{array}\right.$,设方程f(x)=2-x+b(b∈R)的四个实根从小到大依次为x1,x2,x3,x4,对于满足条件的任意一组实根,下列判断中一定正确的为( )
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
3.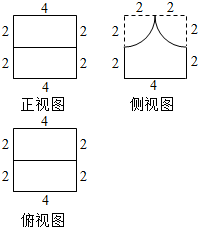 某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )
某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )
 某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )
某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )| A. | 48+4π | B. | 48+8π | C. | 64+4π | D. | 64+8π |
7.函数f(x)=x2-1(2<x<3)的反函数为( )
| A. | f-1(x)=$\sqrt{x-1}$(3<x<8) | B. | f-1(x)=$\sqrt{x+1}$(3<x<8) | C. | f-1(x)=$\sqrt{x-1}$(4<x<9) | D. | f-1(x)=$\sqrt{x+1}$(4<x<9) |
17.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
1.下列命题正确的是( )
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |