题目内容
19.设函数f(x)=sinxcosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$(1)求f(x)的最小正周期及其图象的对称中心;
(2)求函数f(x)的单调递增区间;
(3)求函数f(x)在区间[0,$\frac{π}{2}$]上的最值.
分析 (1)利用二倍角公式和辅助角公式得到f(x)=$sin({2x-\frac{π}{3}})$,易求该函数的最小正周期及其图象的对称中心;
(2)根据正弦函数图象的性质作答;
(3)根据正弦函数图象和函数的定义域解答.
解答 解:(1)$f(x)=\frac{1}{2}sin2x+\sqrt{3}•\frac{1+cos2x}{2}-\frac{{\sqrt{3}}}{2}$
=$\frac{1}{2}sin2x-\frac{{\sqrt{3}}}{2}cos2x$
=$sin({2x-\frac{π}{3}})$,
所以f(x)的最小正周期为$T=\frac{2π}{2}=π$.
令$2x-\frac{π}{3}=kπ({k∈Z})$,得对称中心为$({\frac{kπ}{2}+\frac{π}{6},0})({k∈Z})$;
(2)令$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2}({k∈Z})$,
解得$kπ-\frac{π}{12}≤x≤kπ+\frac{5π}{12}({k∈Z})$,
所以f(x)的单调递增区间为$[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]({k∈Z})$;
(3)∵$0≤x≤\frac{π}{2}∴-\frac{π}{3}≤2x-\frac{π}{3}≤\frac{2π}{3}$,
∴$-\frac{{\sqrt{3}}}{2}≤sin(2x-\frac{π}{3})≤1$,
∴函数的最大值为1,最小值为-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
14.命题“?x0∈∁RQ,x02∈Q”的否定是( )
| A. | ?x0∈∁RQ,x02∈Q | B. | ?x0∈∁RQ,x02∉Q | C. | ?x∉∁RQ,x2∈Q | D. | ?x∈∁RQ,x2∉Q |
11.已知$f(x)=sin\frac{πx}{6}(x∈R)$,则f(1)+f(2)+f(3)+…+f(2017)=( )
| A. | 2017 | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
9.已知f(x)=$\left\{\begin{array}{l}{cosπx,(x<1)}\\{f(x-1),(x≥1)}\end{array}\right.$,求$f({\frac{1}{3}})+f({\frac{4}{3}})$的值( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
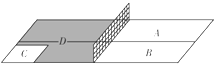 乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:
乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求: