题目内容
14.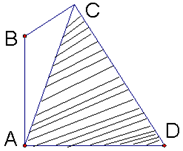 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).(Ⅰ)求灯柱AB的高度(用ξ表示);
(Ⅱ)求灯柱AB与灯杆BC长度之和的最小值,及取最小值时θ的值.
分析 (Ⅰ)由条件求得∠BAC=60°-θ,∠CAD=30°+θ,∠ADC=90°-θ.△ACD中,利用正弦定理求得AC的值,在△ABC中,由正弦定理求得灯柱AB的高度的值.
(Ⅱ)在△ABC中,由正弦定理求得BC的值,再根据 S=AB+BC=8$\sqrt{3}$+16sin(2θ+60°).根据30°≤θ≤45°,利用正弦函数的定义域和值域求得S的最小值.
解答 解:(Ⅰ)∵∠ABC=120°,∠ACB=θ,∴∠BAC=60°-θ,
∵∠BAD=90°,∴∠CAD=30°+θ,
∵∠ACD=60°,∴∠ADC=90°-θ,
在△ACD中,∵$\frac{AD}{sin∠ACD}=\frac{AC}{sin∠ADC}$,∴$AC=\frac{24cosθ}{{sin{{60}°}}}=16\sqrt{3}cosθ$,
在△ABC中,∵$\frac{AB}{sin∠ACB}=\frac{AC}{sinB}$,∴$AB=\frac{ACsinθ}{{sin{{120}°}}}=\frac{{16\sqrt{3}sinθcosθ}}{{sin{{120}°}}}=16sin2θ$,
即灯柱AB的高度为16sin2θ米.…(6分)
(Ⅱ)在△ABC中,∵$\frac{BC}{sin∠BAC}=\frac{AC}{sinB}$,
∴$BC=\frac{{ACsin({{60}°}-θ)}}{{sin{{120}°}}}=32cosθsin({60°}-θ)=8\sqrt{3}+8\sqrt{3}cos2θ-8sin2θ$,
即$AB+BC=8\sqrt{3}+8\sqrt{3}cos2θ+8sin2θ=8\sqrt{3}+16sin(2θ+{60°})$,
∵30°≤θ≤45°,∴120°≤2θ+60°≤150°,
∴当θ=45°时,灯柱AB与灯杆BC长度之和的最小值为$8\sqrt{3}+8$米.…(12分)
点评 本题主要考查正弦定理的应用,三角形的内角和公式,正弦函数的定义域和值域,属于中档题.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | $\frac{18}{25}$ | B. | $-\frac{18}{25}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |
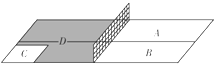 乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:
乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求: