题目内容
10.已知x,y满足不等式组$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$,则满足条件的P(x,y)表示的平面区域的面积等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 作出不等式对应的平面区域,根据平面区域的形状,求出交点坐标,结合三角形的面积公式,建立方程即可得到结论.
解答 解:不等式组对应的平面区域如图: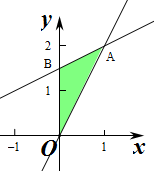
则对应区域为三角形OAB.
由$\left\{\begin{array}{l}{x=0}\\{x-2y+3=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=0}\\{y=\frac{3}{2}}\end{array}\right.$,即B(0,$\frac{3}{2}$),
由$\left\{\begin{array}{l}{2x-y=0}\\{x-2y+3=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,即A(1,2),
则|OB|=$\frac{3}{2}$,
则三角形的面积S=$\frac{1}{2}$×$\frac{3}{2}$×1=$\frac{3}{4}$,
故选:C
点评 本题主要考查二元一次不等式组表示平面区间,考查学生的作图能力,比较基础.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
1.设两点A、B的坐标为A(-1,0)、B(1,0),若动点M满足直线AM与BM的斜率之积为-2,则动点M的轨迹方程为( )
| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | x2-$\frac{{y}^{2}}{2}$=1(x≠±1) | C. | x2+$\frac{{y}^{2}}{2}$=1 | D. | x2+$\frac{{y}^{2}}{2}$=1(x≠±1) |
18.已知四面体ABCD各棱长都等于1,点E,F分别是AB,CD的中点,则异面直线AF与CE所成角的余弦值为( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
5.已知集合M={x|(x+2)(x-3)≤0},N={-3,-1,1,3,5},则M∩N=( )
| A. | {1,3} | B. | {-3,-1,1} | C. | {-3,1} | D. | {-1,1,3} |
2.设Sn是数列{an}的前n项和,且${S_n}=\frac{1}{2}-\frac{1}{2}{a_n}$,则an=( )
| A. | $\frac{1}{3}•{(\frac{1}{2})^{n-1}}$ | B. | $\frac{1}{2}•{(\frac{2}{3})^{n-1}}$ | C. | $2•{(\frac{1}{3})^n}-\frac{1}{3}$ | D. | ${(\frac{1}{3})^n}$ |
19.已知向量$\overrightarrow{a}$=(2,1,4),$\overrightarrow{b}$=(1,0,2),且$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直,则k的值是( )
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{15}{31}$ |
20.某工厂对某产品的产量与成本的资料分析后有如下数据:
则该产品的成本y与产量x之间的线性回归方程为$\stackrel{∧}{y}$=1.10x+4.60.
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |