题目内容
18.已知四面体ABCD各棱长都等于1,点E,F分别是AB,CD的中点,则异面直线AF与CE所成角的余弦值为( )| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 由题意可得四面体A-BCD为正四面体,如图,连接BE,取BE的中点K,连接FK,则FK∥CE,故∠AFK即为所求的异面直线角或者其补角.利用等边三角形的性质、勾股定理、余弦定理即可得出.
解答 解:由题意可得四面体A-BCD为正四面体,如图,连接BE,取BE的中点K,连接FK,则FK∥CE,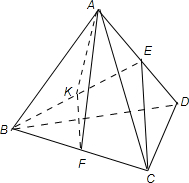
故∠AFK即为所求的异面直线角或者其补角.
不妨设这个正四面体的棱长为2,在△AKF中,AF=$\sqrt{3}$=CE,KF=$\frac{1}{2}$CE=$\frac{\sqrt{3}}{2}$,KE=$\frac{1}{2}$BE=$\frac{\sqrt{3}}{2}$,
AK=$\sqrt{A{E}^{2}+K{E}^{2}}$=$\frac{\sqrt{7}}{2}$,
△AKF中,由余弦定理可得 cos∠AFK=$\frac{A{F}^{2}+F{K}^{2}-A{K}^{2}}{2AF•FK}$=$\frac{2}{3}$.
故选:B.
点评 本题考查了正四面题的性质等边三角形的性质、勾股定理、余弦定理、空间位置关系,考查了推理能力,属于中档题.

练习册系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{|lnx|,0<x≤2}\\{f(4-x),2<x<4}\end{array}$,若当方程f(x)=m有四个不等实根x1,x2,x3,x4(x1<x2<x3<x4)时,不等式kx3x4+x12+x22≥k+11恒成立,则实数k的最小值为 ( )
| A. | $\frac{9}{8}$ | B. | 2-$\frac{\sqrt{3}}{2}$ | C. | $\frac{25}{16}$ | D. | $\sqrt{3}$-$\frac{1}{2}$ |
6.若$\frac{1}{b}$<$\frac{1}{a}$<0,则下列结论不正确的是( )
| A. | a2<b2 | B. | ab>b2 | C. | a+b<0 | D. | |a|+|b|>a+b |
13.执行如图所示的程序框图,输出的S值为( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
10.已知x,y满足不等式组$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$,则满足条件的P(x,y)表示的平面区域的面积等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
7.下列判断错误的是( )
| A. | 命题“?x>1,x2-1>0”的否定是“?x>1,x2-1≤0” | |
| B. | “x=2”是“x2-x-2=0”的充分不必要条件 | |
| C. | 若“p∧q”为假命题,则p,q均为假命题 | |
| D. | 命题“若a•b=0,则a=0或b=0”的否命题为“若a•b≠0,则a≠0且b≠0” |
8.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则∁U(A∩B)=( )
| A. | {1,4,5} | B. | {2,3} | C. | {4,5} | D. | {1,5} |
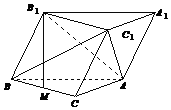 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,M是BC的中点,且BM1⊥BC,平面B1C1CB⊥平面ABC.BC=CA=AA1.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,M是BC的中点,且BM1⊥BC,平面B1C1CB⊥平面ABC.BC=CA=AA1.