题目内容
19．已知向量$\overrightarrow{a}$=（2，1，4），$\overrightarrow{b}$=（1，0，2），且$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直，则k的值是（ ）| A． | 1 | B． | $\frac{1}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{15}{31}$ |
分析 利用向量垂直与数量积的关系即可得出．
解答 解：$\overrightarrow{a}$+$\overrightarrow{b}$=（3，1，6），k$\overrightarrow{a}$-$\overrightarrow{b}$=（2k-1，k，4k-2），
∵$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直，∴3（2k-1）+k+6（4k-2）=0，
解得k=$\frac{15}{31}$，
故选：D．
点评 本题考查了向量垂直与数量积的关系、向量坐标运算性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
10．已知x，y满足不等式组$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$，则满足条件的P（x，y）表示的平面区域的面积等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{\sqrt{2}}{2}$ |
7．下列判断错误的是（ ）
| A． | 命题“?x＞1，x2-1＞0”的否定是“?x＞1，x2-1≤0” | |
| B． | “x=2”是“x2-x-2=0”的充分不必要条件 | |
| C． | 若“p∧q”为假命题，则p，q均为假命题 | |
| D． | 命题“若a•b=0，则a=0或b=0”的否命题为“若a•b≠0，则a≠0且b≠0” |
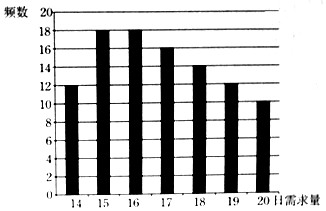某蛋糕店每天制作生日蛋糕若干个，每个生日蛋糕成本为50元，每个蛋糕的售价为100元，如果当天卖不完，剩余的蛋糕作垃圾处理．现搜集并整理了100天生日蛋糕的日需求量（单位：个），得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率．
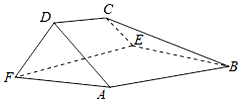如图，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF=2FD，∠AFD=90°，且二面角D-AF-E与二面角C-BE-F都是60°．
11．函数y=1-2x的值域为（ ）
| A． | [1，+∞） | B． | （1，+∞） | C． | （-∞，1] | D． | （-∞，1） |
8．设集合U={1，2，3，4，5}，A={1，2，3}，B={2，3，4}，则∁U（A∩B）=（ ）
| A． | {1，4，5} | B． | {2，3} | C． | {4，5} | D． | {1，5} |