题目内容
1.设两点A、B的坐标为A(-1,0)、B(1,0),若动点M满足直线AM与BM的斜率之积为-2,则动点M的轨迹方程为( )| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | x2-$\frac{{y}^{2}}{2}$=1(x≠±1) | C. | x2+$\frac{{y}^{2}}{2}$=1 | D. | x2+$\frac{{y}^{2}}{2}$=1(x≠±1) |
分析 由题意可得:设M(x,y),写出直线AM与直线BM的斜率分别为 $\frac{y}{x+1}$,$\frac{y}{x-1}$,结合题意得到x与y的关系,进而得到答案.
解答 解:由题意可得:设M(x,y),
所以直线AM与直线BM的斜率分别为 $\frac{y}{x+1}$,$\frac{y}{x-1}$,x≠±1.
因为直线AM与直线BM的斜率之积为-2,
所以 $\frac{y}{x+1}$•$\frac{y}{x-1}$=-2,化简得:x2+$\frac{{y}^{2}}{2}$=1.x≠±1
所以动点M的轨迹E的方程为x2+$\frac{{y}^{2}}{2}$=1(x≠±1).
故选:D.
点评 本题主要考查求曲线轨迹方程的方法,注意x的范围,考查转化思想以及计算能力.

练习册系列答案
相关题目
12.在极坐标系中,点(1,$\frac{π}{4}$)与点(1,$\frac{3π}{4}$)的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
6.若$\frac{1}{b}$<$\frac{1}{a}$<0,则下列结论不正确的是( )
| A. | a2<b2 | B. | ab>b2 | C. | a+b<0 | D. | |a|+|b|>a+b |
13.执行如图所示的程序框图,输出的S值为( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
10.已知x,y满足不等式组$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$,则满足条件的P(x,y)表示的平面区域的面积等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
11.函数y=1-2x的值域为( )
| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,1] | D. | (-∞,1) |
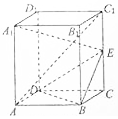 在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证:
在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证: