题目内容
已知顶点在原点开口向右的抛物线C经过定点P（3，2
），斜率为2的直线l交抛物线C于A，B两点，且|AB|=3
，求圆锥曲线C和直线l的方程．
| 3 |
| 5 |
考点：抛物线的标准方程,抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：利用抛物线的定义，可得抛物线方程，直线方程代入抛物线方程，利用韦达定理及弦长公式，即可求得直线方程．
解答：
解：∵顶点在原点开口向右的抛物线C经过定点P（3，2
），
∴y2=2px
即12=2p×3，p=2
∴抛物线方程为y2=4x；
设l的方程为y=2x+b，A（x1y1），B（x2，y2）
由y=2x+b代入y2=4x，消去y，整理得：4x2+4（b-1）x+b2=0，
则x1+x2=-（b-1），x1x2=
，k=2，
∴|AB|=
=
=
又∵|AB|=3
，∴1-2b=9，∴b=-4
故直线?的方程为y=2x-4，
综上所述：圆锥曲线C的方程为y2=4x，直线l的方程为y=2x-4．
| 3 |
∴y2=2px
即12=2p×3，p=2
∴抛物线方程为y2=4x；
设l的方程为y=2x+b，A（x1y1），B（x2，y2）
由y=2x+b代入y2=4x，消去y，整理得：4x2+4（b-1）x+b2=0，
则x1+x2=-（b-1），x1x2=
| b2 |
| 4 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x 1x2] |
| (1+k2)[(b-1)2-b2] |
| (1+k2)(1-2b) |
又∵|AB|=3
| 5 |
故直线?的方程为y=2x-4，
综上所述：圆锥曲线C的方程为y2=4x，直线l的方程为y=2x-4．
点评：本题考查抛物线的定义，考查直线与圆锥曲线的位置关系，考查弦长的计算，属于中档题．
练习册系列答案
相关题目
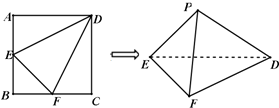如图，在边长为2的正方形ABCD中，E，F分别是AB，BC的中点，将△AED，△BEF，△CFD分别沿DE，EF，DF折起，使A，B，C三点重合于点P．