题目内容
定义在R上的函数f（x）既是奇函数又是以2为周期的周期函数，则f（1）等于 ．
考点：周期函数,函数奇偶性的性质
专题：函数的性质及应用
分析：根据奇函数和周期函数的性质可以知道，由于定义在R上的函数f（x）是奇函数，又是以2为周期的周期函数，可得-f（1）=f（-1）=f（-1+2）=f（1），f（1）=0．
解答：
解：由于定义在R上的函数f（x）是奇函数，又是以2为周期的周期函数，
所以-f（1）=f（-1）=f（-1+2）=f（1），
所以f（1）=0．
故答案为：0．
所以-f（1）=f（-1）=f（-1+2）=f（1），
所以f（1）=0．
故答案为：0．
点评：本题主要考查奇函数和周期函数的定义，考查学生的推理能力．
练习册系列答案
相关题目
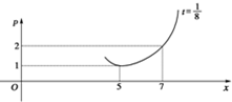我国加入WTO时，根据达成的协议，若干年内某产品市场供应量p与关税的关系近似满足p（x）=2（1-kt）（x-b）2（其中t为关税的税率，且t∈[0，