题目内容
使数列{an}的前五项依次是1,2,4,7,11的一个通项公式是an=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:a2-a1=2-1=1,a3-a1=4-2=2,a4-a3=7-4=3,a5-a4=11-7=4,…,可得an-a1=1+2+3+…+(n-1),再利用等差数列的前n项和公式即可得出.
解答:
解:a2-a1=2-1=1,
a3-a1=4-2=2,
a4-a3=7-4=3,
a5-a4=11-7=4,
…,
∴an-a1=1+2+3+…+(n-1)=
.
∴an=
.
故选:A.
a3-a1=4-2=2,
a4-a3=7-4=3,
a5-a4=11-7=4,
…,
∴an-a1=1+2+3+…+(n-1)=
| n(n-1) |
| 2 |
∴an=
| n2-n+2 |
| 2 |
故选:A.
点评:本题考查了等差数列的前n项和公式、“累加求和”方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知y=f(x)在(0,3)上是增函数,函数f(x+3)是偶函数,则( )
A、f(
| ||||
B、f(
| ||||
C、f(4)<f(
| ||||
D、f(
|
某校为了了解1500名学生对学校食堂的意见,从中抽取1个容量为50的样本,采用系统抽样法,则分段间隔为( )
| A、10 | B、15 | C、20 | D、30 |
 如图,AD⊥CD,AC⊥BC,AB=4,AD=CD=2,M为线段AB的中点,平面ACD⊥平面ABC.
如图,AD⊥CD,AC⊥BC,AB=4,AD=CD=2,M为线段AB的中点,平面ACD⊥平面ABC.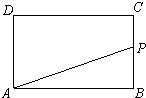 如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).
如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).