题目内容
自点M（2，4）作圆（x-1）2+（y+3）2=1的切线l，求切线l的方程．
考点：圆的切线方程
专题：直线与圆
分析：切线的斜率不存在时x=3验证即可，当切线的斜率存在时，设为k，写出切线方程，圆心到切线的距离等于半径，解出k求出切线方程．
解答：
解：∵圆C：（x-1）2+（y+3）2=1．圆的圆心坐标（1，-3），半径为1，
当切线的斜率不存在时，对直线x=2，C（1，-3）到直线的距离为1，满足条件；
当k存在时，设直线y-4=k（x-2），即y=kx+4-2k，
∴
=1，得k=
．
∴得直线方程x=2或y=
x-
．
故切线的方程为x=2或24x-7y-20=0．
当切线的斜率不存在时，对直线x=2，C（1，-3）到直线的距离为1，满足条件；
当k存在时，设直线y-4=k（x-2），即y=kx+4-2k，
∴
| |7-k| | ||
|
| 24 |
| 7 |
∴得直线方程x=2或y=
| 24 |
| 7 |
| 20 |
| 7 |
故切线的方程为x=2或24x-7y-20=0．
点评：本题考查圆的切线方程，点到直线的距离公式，是基础题．
练习册系列答案
相关题目
使数列{an}的前五项依次是1，2，4，7，11的一个通项公式是an=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若f′（x0）=-3，则
=（ ）
| lim |
| h→0 |
| f(x0+h)-f(x0-h) |
| h |
| A、-3 | B、-6 | C、-9 | D、-12 |
在公比为整数的等比数列{an}中，若，a1+a3=6，a2+a4=12，则a3等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
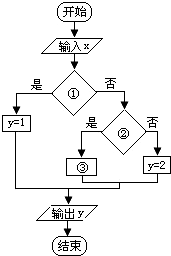任给x的值，计算函数y=
|
| A、x＜1、x＞1、y=3 |
| B、x=1、x＞1、y=3 |
| C、x＜1、x=1、y=3 |
| D、x＜1、x＞1、y=3 |
