Question

如图，AD⊥CD，AC⊥BC，AB=4，AD=CD=2，M为线段AB的中点，平面ACD⊥平面ABC．
（1）求证：BC⊥平面ACD；
（2）求二面角D-CM-A的正切值；
（3）求异面直线AC与BD成角的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题

专题：空间位置关系与距离

分析：（1）要证明BC⊥平面ACD．我们根据可以根据已知中侧面ADC⊥底面ABC．结合平面与平面垂直的性质定理进行证明，即只要说明AC⊥BC即可，
（2）由（1）的结论，取AC的中点为O，连接DO，OM．建立空间直角坐标系O-xyz，然后利用空间向量法，进行求解．
（3）要求异面直线BD与CM所成角的余弦值，我们只要求

AC

与

BD

夹角余弦值的绝对值即可．

解答： 证明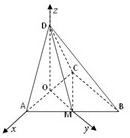：（1）∵AC⊥BC，平面ADC⊥平面ABC，平面ADC∩平面ABC=AC，BC?平面ABC，
∴BC⊥平面ACD．
解：（2）取AC的中点为O，连接DO，OM，建立空间直角坐标系O-xyz如图所示．
∵AD⊥CD，AC⊥BC，AB=4，AD=CD=2，M为线段AB的中点，
∴OA=OC=OM=OD=

2

，
则A（

2

，0，0），C（-

2

，0，0），D（0，0，

2

），B（-

2

，2

2

，0），M（0，

2

，0）．
∴

CD

=（

2

，0，

2

），

CM

=（

2

，

2

，0），
令

m

=（x，y，z）是平面DCM的一个法向量，
则

m ⊥ CD m ⊥ CM

，即

m • CD =0 m • CM =0

，
即

2 x+ 2 z=0 2 x+ 2 y=0

，
令x=1，则平面DCM的法向量为

m

=（1，-1，-1），
∵AD=CD，O为AC的中点，
∴OD⊥AC，
又∵平面ADC⊥平面ABC，平面ADC∩平面ABC=AC，OD?平面ACD，
∴OD⊥平面ABC，即OD⊥平面ACM，
即

OD

=（0，0，

2

）为平面ACM的一个法向量，
设锐二面角D-CM-A的平面角为θ，
则cosθ=

| m • OD |

| m |•| OD |

=

6

3

，
则sinθ=

3

3

，tanθ=

2

2

，
即二面角D-CM-A的正切值为

2

2

．
（3）异面直线AC与BD的方向向量分别为：

AC

=（-2

2

，0，0），

BD

=（

2

，-2

2

，

2

），
所以异面直线BD与AC所成角的余弦值为：

| AC • BD |

| AC |•| BD |

=

6

6

点评：本题考查的知识点是与二面角有关的立体几何问题，建立空间坐标系，将二面角问题和异面直线问题转化为向量夹角问题，是解答的关键，难度中档．