题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<0}\\{|\frac{1}{2}{x}^{2}-2x+1|,x≥0}\end{array}\right.$,方程f2(x)-af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )| A. | [6,11] | B. | [3,11] | C. | (6,11) | D. | (3,11) |
分析 作函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<0}\\{|\frac{1}{2}{x}^{2}-2x+1|,x≥0}\end{array}\right.$的图象,从而利用数形结合知t2-at+b=0有2个不同的正实数解,且其中一个为1,从而可得-1-a>0且-1-a≠1;从而解得.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<0}\\{|\frac{1}{2}{x}^{2}-2x+1|,x≥0}\end{array}\right.$的图象如下,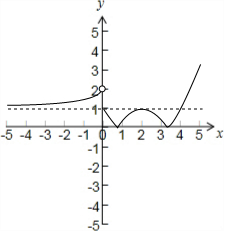
∵关于x的方程f2(x)-af(x)+b=0有6个不同实数解,
令t=f(x),
∴t2-at+b=0有2个不同的正实数解,
其中一个为在(0,1)上,一个在(1,2)上;
故$\left\{\begin{array}{l}b>0\\ 1-a+b<0\\ 4-2a+b>0\end{array}\right.$,
其对应的平面区域如下图所示: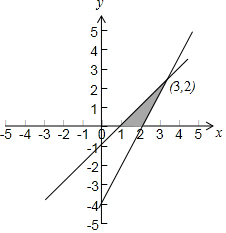
故当a=3,b=2时,3a+b取最大值11,
当a=1,b=0时,3a+b取最小值3,
则3a+b的取值范围是(3,11)
故选:D
点评 本题考查了数形结合的思想应用及分段函数的应用,同时考查了线性规划,难度中档.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
11.已知集合A={x|2x2+x-3=0},集合B={i|i2≥4}},∁RC={-1,1,$\frac{3}{2}$},则A∩BU∁RC=( )
| A. | {1,-1,$\frac{3}{2}$} | B. | {-2,1,-$\frac{3}{2}$,-1} | C. | {1} | D. | {2,1,-1,$\frac{3}{2}$} |
12.不等式$\frac{ax+1}{x+b}>1$的解集为(-∞,-1)∪(3,+∞),则不等式x2+bx-2a<0的解集为( )
| A. | (-2,5) | B. | (-0.5,0.2) | C. | (-2,1) | D. | (-0.5,1) |
2.在平面直角坐标系中,已知三点A(1,-2),B(2,-1),C(0,-2),则|$\overrightarrow{AB}$+$\overrightarrow{BC}$|=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.化简$\sqrt{1-2sin1cos1}$的结果为( )
| A. | sin1-cos1 | B. | cos1-sin1 | C. | sin1+cos1 | D. | -sin1-cos1 |
19.已知集合A={x|x>5},集合B={x|x>a},若命题“x∈A”是命题“x∈B”的充分不必要条件,则实数a的取值范围是( )
| A. | (-∞,5) | B. | (-∞,5] | C. | (5,+∞) | D. | [5,+∞) |