题目内容
6.(Ⅰ)解关于x的一元二次不等式x(x-2)-3>0;(Ⅱ)解关于x的一元二次不等式(x-4)(x-2a)<0(其中a∈R).
分析 (Ⅰ)先求出x2-2x-3>0,由此能求出关于x的一元二次不等式x(x-2)-3>0的解集.
(Ⅱ)由当2a>4,即a>2,2a<4,即a<2,2a=4,即a=2三种情况进行分类讨论,由此能求出关于x的一元二次不等式(x-4)(x-2a)<0(其中a∈R)的解集.
解答 解:(Ⅰ)∵x(x-2)-3>0,
∴x2-2x-3>0,
解方程x2-2x-3=0,得x1=-1,x2=3,
∴关于x的一元二次不等式x(x-2)-3>0的解集为{x|x<-1或x>3}.
(Ⅱ)∵(x-4)(x-2a)<0(其中a∈R),
∴(x-4)(x-2a)=0的解为x1=4,x2=2a,
∴当2a>4,即a>2时,
关于x的一元二次不等式(x-4)(x-2a)<0为{x|4<x<2a};
当2a<4,即a<2时,
关于x的一元二次不等式(x-4)(x-2a)<0为{x|2a<x<4};
当2a=4,即a=2时,
关于x的一元二次不等式(x-4)(x-2a)<0为∅.
点评 本题考查一元二次方程的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
16.一个三棱锥的三视图如图所示,则该三棱锥的体积为( )
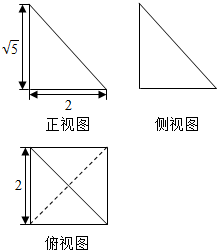

| A. | $\frac{2\sqrt{5}}{3}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
14.直线l过定点(-1,2)且在两坐标轴上的截距相等,则直线l的方程为( )
| A. | 2x+y=0或x+y-1=0 | B. | 2x-y=0或x+y-1=0 | ||
| C. | 2x+y=0或x-y+3=0 | D. | x+y-1=0或x-y+3=0 |
1.已知{an}是等差数列,{bn}是等比数列,bn>0恒成立,若a2=b2且a8=b8,则( )
| A. | a5≥b5 | B. | a5≤b5 | C. | a5>b5 | D. | a5<b5 |
16.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,Q为右支上一点,P点在直线x=-a上,且满足$\overrightarrow{PQ}$=$\overrightarrow{Q{F}_{2}}$,$\overrightarrow{OQ}$=λ($\frac{\overrightarrow{O{F}_{2}}}{|\overrightarrow{O{F}_{2}}|}$+$\frac{\overrightarrow{OP}}{|\overrightarrow{OP}|}$)(λ≠0),则该双曲线的离心率为( )
| A. | $\sqrt{5}$+1 | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$ |
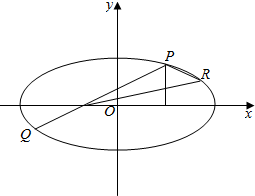 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点为F1、F2,过F2作垂直于x轴的直线交椭圆于P点(点P在x轴上方),连结PF1并延长交椭圆于另一点Q.设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$(2≤λ≤$\frac{7}{3}$).
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点为F1、F2,过F2作垂直于x轴的直线交椭圆于P点(点P在x轴上方),连结PF1并延长交椭圆于另一点Q.设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$(2≤λ≤$\frac{7}{3}$).