题目内容
1.已知{an}是等差数列,{bn}是等比数列,bn>0恒成立,若a2=b2且a8=b8,则( )| A. | a5≥b5 | B. | a5≤b5 | C. | a5>b5 | D. | a5<b5 |
分析 设公差为d,公比为q,作差比较,运用因式分解,即可得出结论.
解答 解:设公差为d,公比为q,则
∵a2=b2,a8=b8,
∴a2+6d=a2q6,∴d=$\frac{1}{6}$a2(q6-1)
∴a5-b5=a2+3d-a2q3=a2(1-q3)+$\frac{1}{2}$a2(q6-1)
=$\frac{1}{2}$a2(q3-1)2,
∵a2>0,(q3-1)2≥0,
∴$\frac{1}{2}$a2(q3-1)2≥0,
即有a5≥b5,
故选:A.
点评 本题考查等差数列与等比数列的通项公式的运用以及作差法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设条件p:-1<x<5,条件q:0<x<a,其中a为正数,若p是q的必要不充分条件,则a的取值范围为( )
| A. | (0,5] | B. | (0,5) | C. | [5,+∞) | D. | (5,+∞) |
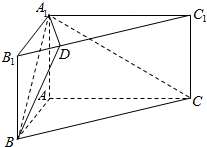 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.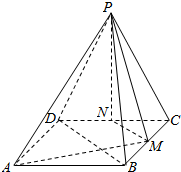 如图,在四棱锥P-ABCD中,侧面PCD丄底面ABCD,△PCD为等边三角形,M为BC中点,N为CD中点.若底面ABCD是矩形且AD=2$\sqrt{2}$,AB=2.
如图,在四棱锥P-ABCD中,侧面PCD丄底面ABCD,△PCD为等边三角形,M为BC中点,N为CD中点.若底面ABCD是矩形且AD=2$\sqrt{2}$,AB=2.