函数f(x)=x+sinx的图象在点O(0.0)处的切线方程是y=2x．题目和参考答案——青夏教育精英家教网——

题目内容

17．函数f（x）=x+sinx的图象在点O（0，0）处的切线方程是y=2x．

分析求出函数的导数，求得切线的斜率，由点斜式方程可得切线的方程．

解答解：函数f（x）=x+sinx的导数为f′（x）=1+cosx，
即有图象在点O（0，0）处的切线斜率为k=1+cos0=2，
则图象在点O（0，0）处的切线方程为y=2x．
故答案为：y=2x．

点评本题考查导数的运用：求切线的方程，考查直线方程的运用，正确求导是解题的关键．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

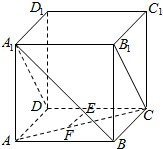如图，正方体ABCD-A₁B₁C₁D₁中，E是A₁B上的点，F是AC上的点，且A₁E=2EB，CF=2AF．求证：EF∥平面A₁B₁CD．

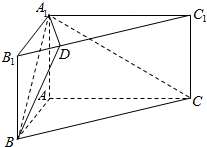8．已知集合M={x|-1≤x≤7}，集合N={x|k+1≤x≤2k-1}，若M∩N=∅，求k的取值范围．

5．化简$\sqrt{1-si{n}^{2}160°}$=（　　）

如图，在直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，$AC=2\sqrt{3}$，$A{A_1}=\sqrt{3}$，AB=2，点D在棱B₁C₁上，且B₁C₁=4B₁D．
（Ⅰ）求证：BD⊥A₁C；
（Ⅱ）求二面角B-A₁D-B₁的大小．

2．已知数列{a_n}，对于任意n∈N^*，都有a_n=n²-bn，是否存在一个整数m，使得当b＜m时，数列{a_n}为递增数列？这样的整数是否唯一？是否存在最大的整数？

9．设数列{a_n}的前n项和为S_n，已知S_n+1=pS_n+q（n∈N^*，p，q为常数），a₁=2，a₂=1，a₃=q-3p．
（1）求p，q的值；
（2）求数列{a_n}的通项公式；
（3）记集合M={n|λ≥$\frac{{S}_{n}}{n{a}_{n}}$，n∈N^*}，若M中仅有3个元素，求实数λ的取值范围．

6．（Ⅰ）解关于x的一元二次不等式x（x-2）-3＞0；
（Ⅱ）解关于x的一元二次不等式（x-4）（x-2a）＜0（其中a∈R）．

7．已知集合A={0，1}，B={-1，0，a²+a-1}，且A⊆B，则a等于（　　）