题目内容
15.设O是△ABC的外心,a,b,c分别为角A,B,C对应的边,已知b2-2b+c2=0,则$\overrightarrow{{B}C}•\overrightarrow{{A}{O}}$的范围是( )| A. | $({-\frac{1}{4},2}]$ | B. | $[{-\frac{1}{4},2})$ | C. | $[{-2,\frac{1}{4}})$ | D. | $({-2,\frac{1}{4}}]$ |
分析 根据已知条件可画出△ABC及其外接圆,连接AO并延长,交外接圆于D.所以便得到cos∠BAD=$\frac{AB}{AD}$,cos∠CAD=$\frac{AC}{AD}$,根据数量积得到$\overrightarrow{{B}C}•\overrightarrow{{A}{O}}$=(b-$\frac{1}{2}$)2-$\frac{1}{4}$,而根据c2=2b-b2可求得b的范围0<b<2,所以求出二次函数$f(b)={({b-\frac{1}{2}})^2}-\frac{1}{4}$在(0,2)上的范围即可.
解答 解: O是△A BC 的三边中垂线的交点,故O是三角形外接圆的圆心,如图所示,延长AO交外接圆于D.AD是⊙O的直径,
O是△A BC 的三边中垂线的交点,故O是三角形外接圆的圆心,如图所示,延长AO交外接圆于D.AD是⊙O的直径,
所以∠ACD=∠ABD=90°,
$cos∠C{A}D=\frac{{{A}C}}{{{A}D}}$,$cos∠{B}{A}D=\frac{{{A}{B}}}{{{A}D}}$,
所以$\overrightarrow{{A}{O}}•\overrightarrow{{B}C}=\frac{1}{2}\overrightarrow{{A}D}•({\overrightarrow{{A}C}-\overrightarrow{{A}{B}}})=\frac{1}{2}\overrightarrow{{A}D}•\overrightarrow{{A}C}-\frac{1}{2}\overrightarrow{{A}D}•\overrightarrow{{A}{B}}$,
=$\frac{1}{2}{|{\overrightarrow{{A}C}}|^2}-\frac{1}{2}{|{\overrightarrow{{A}{B}}}|^2}=\frac{1}{2}{b^2}-\frac{1}{2}{c^2}=\frac{1}{2}{b^2}-\frac{1}{2}({2b-{b^2}})={b^2}-b={({b-\frac{1}{2}})^2}-\frac{1}{4}$,
因为c2=2b-b2>0,
所以0<b<2,
令$f(b)={({b-\frac{1}{2}})^2}-\frac{1}{4}$,
所以当$b=\frac{1}{2}$ 时,有最小值$-\frac{1}{4}$.
因为f(0)=0,f(2)=2,
所以$-\frac{1}{4}≤f(b)<2$,
所以$\overrightarrow{{B}C}•\overrightarrow{{A}{O}}$ 的范围是$[{-\frac{1}{4},2})$.
故选:B.
点评 本题考查圆的直径所对的圆周角为90°,用直角三角形的边表示余弦值,以及二次函数值域的求法,注意解题方法的积累,属于中档题.

 优生乐园系列答案
优生乐园系列答案| A. | B2=AC | B. | A+C=2B | C. | B(B-A)=A(C-A) | D. | B(B-A)=C(C-A) |
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
| A. | y=sinx,x∈R | B. | y=x2,x∈R | C. | y=x-$\frac{1}{x}$,x≠0 | D. | y=2-x,x∈R |
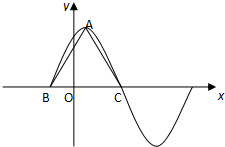 已知f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,点A为图象的最高点,B,C为图象与x轴的交点,且三角形ABC的面积为$\frac{\sqrt{3}}{4}$π.
已知f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,点A为图象的最高点,B,C为图象与x轴的交点,且三角形ABC的面积为$\frac{\sqrt{3}}{4}$π.